数值计算方法第2章作业

第二章

一．问题综述：

二．问题分析：

依题意，均质梁的最大挠度值在满足dy

dx

=0时达到，即：

dy dx =

ω0

120EIL

(?5x4+6L2x2?L4)=0

简单进行化简可得需要求解的非线性方程：

?5x4+6L2x2?L4=0

其中，由已知，L=600cm。

观察方程，可得：

?5(x2)2+6L2(x2)?L4=0

这样可以解出精确解，由二次方程求根公式：

x2=

?6L2±√36L4?20L4

解得：x2=360000cm2或72000cm2。由于是一个实际问题，所以显然可知x>0，即可求得x=600cm 或120√5cm≈268.328157299975cm。此即为真值，求解本题时可以利用所求出的真值进行迭代过程中的相对误差的计算。

三．问题解决：

1.二分法

二分法是通过不断取求根区间的中点，然后根据中点的函数值与求根区间两端点的函数值的正负关系来判断根的位置，从而逐渐缩小求根区间，最终求得数值方法下精度允许的解。

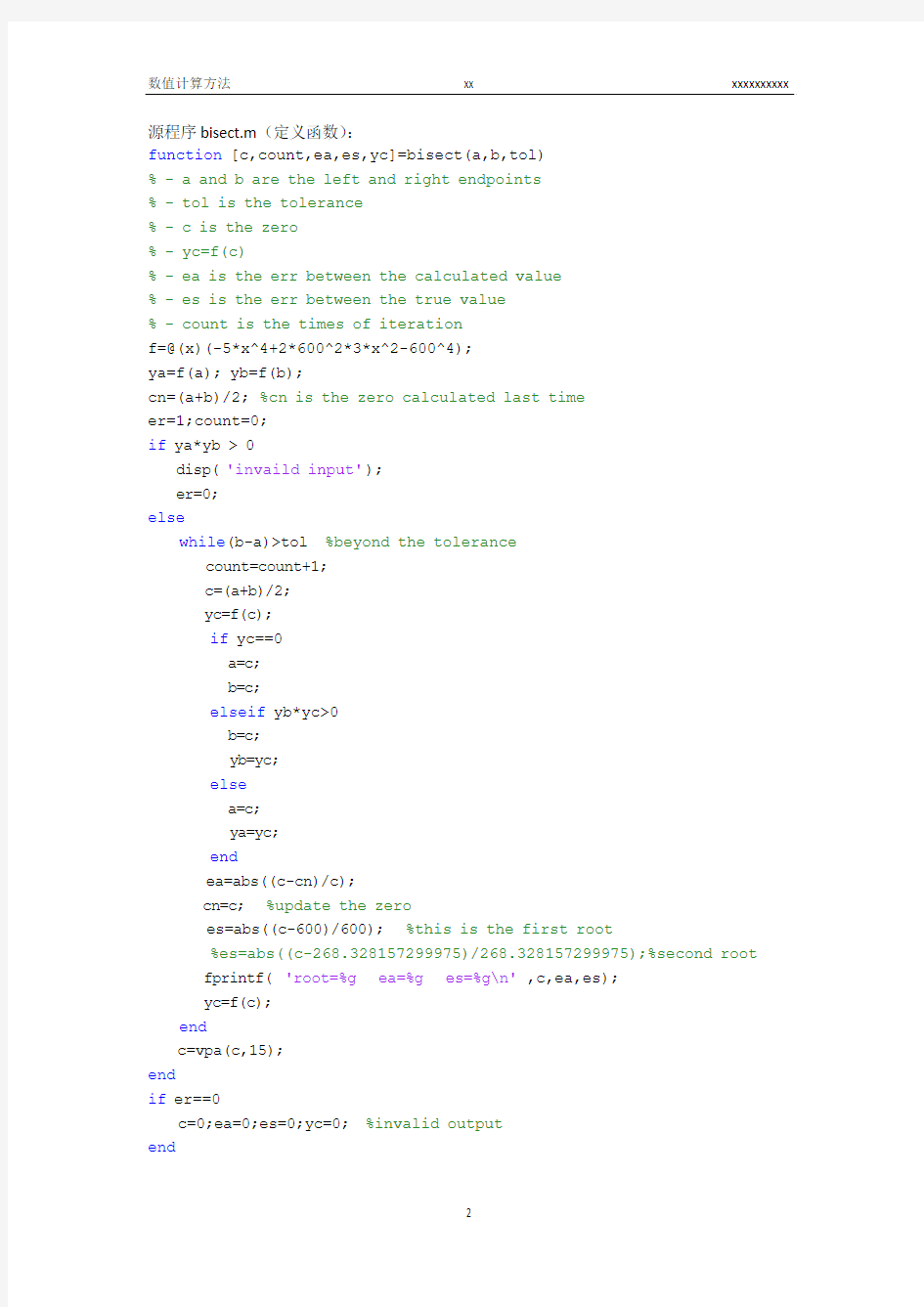
源程序bisect.m（定义函数）：

function [c,count,ea,es,yc]=bisect(a,b,tol)

% - a and b are the left and right endpoints

% - tol is the tolerance

% - c is the zero

% - yc=f(c)

% - ea is the err between the calculated value

% - es is the err between the true value

% - count is the times of iteration

f=@(x)(-5*x^4+2*600^2*3*x^2-600^4);

ya=f(a); yb=f(b);

cn=(a+b)/2; %cn is the zero calculated last time

er=1;count=0;

if ya*yb > 0

disp('invaild input');

er=0;

else

while(b-a)>tol %beyond the tolerance

count=count+1;

c=(a+b)/2;

yc=f(c);

if yc==0

a=c;

b=c;

elseif yb*yc>0

b=c;

yb=yc;

else

a=c;

ya=yc;

end

ea=abs((c-cn)/c);

cn=c; %update the zero

es=abs((c-600)/600); %this is the first root

%es=abs((c-268.328157299975)/268.328157299975);%second root fprintf('root=%g ea=%g es=%g\n',c,ea,es);

yc=f(c);

end

c=vpa(c,15);

end

if er==0

c=0;ea=0;es=0;yc=0; %invalid output

end

使用不同的输入值进行迭代，可得：

表1.二分法计算结果

3 590 620 1e-13 47 600.0 3.7896e-16 0 0

4 590 620 1e-10 39 600.000000000018 9.0949e-14 3.0316e-14 -0.0315

5 590 620 1e-5 22 599.999997615814 1.1921e-08 3.9736e-09 4.1199e+03

迭代过程篇幅过长，此处略去，只保留每次使用函数迭代后的输出结果。从迭代过程中可以看出二分法在处理此类两端异号的连续函数时，能够迅速地找到方程根的范围，但是在要求精度较高的情况下时，根的收敛的速度会大大下降，这个现象可以通过资料中的迭代次数公式:

n=?log2(x r?x l E a,d

)?

求得。但是进行二分法的前提是必须知道每一个根的区间，所以当方程较复杂时，二分法就不是很适用了。从迭代过程中还可以看出，计算值与真实值的相对误差始终小于近似相对误差，这是有相应理论支持的，所以在实际计算过程中，有时可以通过设置近似相对误差限来保证精度要求。

2.试位法

试位法是通过不断求求根区间两端连线与x轴的交点，并比较此交点的函数值与边界点处的函数值，从而判断根的位置，缩小求根区间，最终求得所要求的精度允许的解。

源程序regula.m（定义函数）：

function [c,count,ea,es,yc]=regula(a,b,delta,epsilon)

% - a and b are the left and right endpoints

% - tol is the tolerance of right and left

% - epsilon is the tolerance of yc and 0

% - c is the zero

% - yc=f(c)

% - ea is the err between the calculated value

% - es is the err between the true value

% - count is the times of iteration

f=@(x)(-5*x^4+2*600^2*3*x^2-600^4);

ya=f(a);yb=f(b);

cn=b-yb*(a-b)/(ya-yb); %cn is the zero calculated last time

c=cn;yc=f(c);er=1;count=0;

if ya*yb > 0

disp('invaild input');

er=0;

else

while((b-a)>delta && abs(yc)>epsilon)

count=count+1;

c=b-yb*(a-b)/(ya-yb);

yc=f(c);

if yb*yc>0

b=c;

yb=yc;

else

a=c;

ya=yc;

end

ea=abs((c-cn)/c);

cn=c; %update zero

es=abs((c-600)/600); %this is the first root

%es=abs((c-268.328157299975)/268.328157299975);%the second

root

fprintf('root=%g ea=%g es=%g\n',c,ea,es);

end

c=vpa(c,15);

end

if er==0

c=0;ea=0;es=0;yc=0; %invalid output

end

使用不同的输入值进行迭代，可得：

表2.试位法计算结果

3 550 700 1e-2 1e-2 30 600.0 1.2127e-1

4 6.8212e-1

5 0.0071

4 590 620 1e-13 1e-13 14 600.0 7.5791e-16 0 0

5 590 620 1e-10 1e-10 14 600.0 7.5791e-1

6 0 0

6 590 620 1e-2 1e-2 10 600.0 7.2191e-14 7.5791e-15 0.0078

2.4723e-11 6.3553e-16 4.5776e-05 7 200 300 1e-8 1e-8 4 268.3281572

99975

8 200 300 1e-4 1e-4 4 268.3281572

2.4723e-11 6.3553e-16 4.5776e-05

99975

9 200 300 1e-2 1e-2 3 268.3281572

1.3600e-05

2.4724e-11 -5.1266

93341

从迭代过程中可以看出试位法相比于二分法能更迅速找到方程根的范围，有时候甚至迭

代区区几次就能达到相当高的精度。但是试位法有一个很大的缺陷，就是当有一个划界点保

持不动时，可能会导致很差的收敛性，并且会严重影响算法效率。

3.改进试位法

试位法的缺陷就是当一个划界点保持不动时，会由于此方法所利用的原理，导致收敛性极差，会使收敛速度大大地下降。而改进的试位法的原理就是通过计数器来检测划界点是否保持不变。如果出现了连续两次保持不变的情况，就将停滞的划界点的函数值变为原来的一半，再继续带入迭代。基于此思想，这里采用增加一个总计数器和两个划界点计数器的方法来实现检测某划界点是否连续两次保持不变。当总计数器到达2次时，判断是否有某个划界点的计数器也到达2次，若有，对其函数值减半；若无，则判断下次计数器到达2次时，是否有此情况。以下源程序中特别标注的部分就是改进的部分。

源代码regula2.m（定义函数）：

function [c,count,ea,es,yc]=regula2(a,b,tol,epsilon)

% - a and b are the left and right endpoints

% - tol is the tolerance of right and left

% - epsilon is the tolerance of yc and 0

% - c is the zero

% - yc=f(c)

% - ea is the err between the calculated value

% - es is the err between the true value

% - count is the times of iteration

f=@(x)(-5*x^4+2*600^2*3*x^2-600^4);

ya=f(a); yb=f(b);

cn=b-yb*(a-b)/(ya-yb); %cn is the zero calculated last time

c=cn;yc=f(c);er=1;count=0;

call=0;ca=0;cb=0; %the counters

if ya*yb > 0

disp('invaild input');

er=0;

else

while((b-a)>tol && abs(yc)>epsilon)

c=b-yb*(a-b)/(ya-yb);

yc=f(c);

if yb*yc>0

b=c;

yb=yc;

call=call+1;

ca=ca+1;

if call==2

if ca==2 %if ca not change two times, let ya be half of ya

ya=ya/2;

end

call=1;

ca=1; %if not change, let it be 1

cb=0; %clear another counter

end

else

a=c;

ya=yc;

call=call+1;

cb=cb+1;

if call==2

if cb==2 %if cb not change two times, let yb be half of yb

yb=yb/2;

end

call=1;

cb=1; %if not change, let it be 1

ca=0; %clear another counter

end

end

ea=abs((c-cn)/c);

cn=c; %update zero

es=abs((c-600)/600); %the first root

%es=abs((c-268.328157299975)/268.328157299975);% the second root

fprintf('root=%g ea=%g es=%g\n',c,ea,es);

count=count+1;

end

c=vpa(c,15);

end

if er==0

c=0;ea=0;es=0;yc=0; %invalid output

end

由于本例中并没有某一个划界点保持不动，所以直接运行改进程序所得的结果和原来的程序基本一致，看不出所改善之处。为验证改动后的函数，采用书上的例子y=x10?1进行尝试，程序中f=@(x)(x^10-1)，根区间取课件上所取的[0,1.3]：

表3.改进试位法计算结果与对比

9907

由上表可以看出，改进法对于有某一个划界点保持不动的情况具有很好的优化效果，可以使试位次数大量减少，大量减少所需计算时间，对原算法进行了极好的优化。

4.不动点法

不动点法就是利用所给的函数或方程f(x)=0来构造函数x=g(x)，函数g(x)的一个不动点(Fixed point)是指一个实数P，满足P=g(P)，利用迭代过程：p n+1=g(p n)解方程f(x)根的过程方法。

源代码fixpt.m（函数定义）：

function [k,p,ea,es,P] = fixpt(p0,tol,max1)

% Input- p0 is the initial guess for the fixed-point

% - tol is the tolerance

% - max1 is the maximum number of iterations

% Output - k is the number of iterations that were carried out

% - p is the approximation to the fixed-point

% - ea is the error in the approximation

% - es is the error between the true value

% - P'contains the sequence {pn}

%g=@(x)(600^2/(sqrt(-5*x^2+6*600^2))); %first transformation

%g=@(x)(sqrt((600^4+5*x^4)/(6*600^2))); %second transformation

g=@(x)(sqrt(sqrt((6*600^2*x^2-600^4)/5))); %third transformation

P(1)= p0;

for k=2:max1

P(k)=feval(g,P(k-1));

ea=abs(P(k)-P(k-1));

relerr=ea/(abs(P(k))+eps);

p=P(k);

if (ea

end

es=abs((P(k)-600)/600); %this is the first root

%es=abs((P(k)-268.328157299975)/268.328157299975);%second root

if k == max1

disp('maximum number of iterations exceeded')

end

p=vpa(p,15);

P=P';

代码中使用了三种变换:x=

2

√?5x2+6L2

、x=L

4

?5x3+6L2x

、x=√6L2x2?L4

5

4

，由

于所求非线性方程有两个相异根，而利用不动点法每个不动点只能收敛到其中一个根，所以需要构造大于等于两个g(x)，才能分别得到两个根。本程序中，第一个和第二个变换都分别能够收敛到268.328157299975，第三个变换能够收敛到600。下表中method即为使用变换公式的次序。

表4.不动点法计算结果

2 700 1e-8 100 37 600.000000889827 5.9322e-07 1.4830e-09 3

3 100 1e-8 100 37 599.999999549696 5.8136e-06 1.4534e-08 3

4 400 1e-12 100 19 268.328157300037 2.4755e-10 2.3006e-13 1

5 400 1e-8 100 14 268.328157493411 7.7375e-07 7.2090e-10 1

6 800 1e-8 100 15 268.328157121611 7.1345e-0

7 6.6472e-10 1

7 400 1e-12 100 28 268.328157300032 1.1454e-10 2.1269e-13 2

8 400 1e-8 100 19 268.328158427351 2.2548e-06 4.2015e-09 2

从表中可以看出，对于每种变换的g(x)，无论输入的初始猜测根p0为多少，都只能收敛到同一个根（2、3或5、6对照），这是不动点法的基本原理造成的。对于收敛到同一个根的两种不同的g(x)，同样的p0，其迭代次数也不相同（4、7或5、8对照），在此题中，method1的迭代效果要优于method2。

5. Newton-Raphson方法

由理论分析可知，不动点迭代方法优化后就是Newton-Raphson方法，于是在此仅对Newton-Raphson方法进行讨论。

由

f(x i+1)?f(x i)+f′(x i)(x i+1?x i)

当其与x轴相交时

f(x i)+f′(x i)(x i+1?x i)=0

所以

x i+1=x i?f(x i) (i)

即为迭代公式。

源代码newton.m（函数定义）：

function [p0,c,ea,es,y]=newton(p0,tol,epsilon)

% Input - p0 is the initial guess for the zero

% - tol is the tolerance

% - epsilon is the tolerance of y and 0

% Output - p0 is the zero

% - y=f(p0)

% - c is the times of iteration

% - ea is the error in the approximation

% - es is the error between the true value

f=@(x)(-5*x^4+2*600^2*3*x^2-600^4);

df=@(x)(-20*x^3+4*600^2*3*x); %df is the differential of f p1=p0-feval(f,p0)/feval(df,p0); %newton iteration

y=f(p0);

p=p0; %last estimated zero

c=0;

while (abs(p1-p0)>tol && abs(y)>epsilon)

c=c+1;

p0=p1;

p1=p0-f(p0)/df(p0);

ea=abs((p0-p)/p0);

p=p0; %update zero

es=abs((p0-600)/600); %the first root

%es=abs((p0-268.328157299975)/268.328157299975);%second root

fprintf('root=%g ea=%g es=%g\n',p0,ea,es);

y=f(p0);

end

p0=vpa(p0,15);

表5. Newton-Raphson方法计算结果

由迭代过程可以看出，Newton-Raphson方法相对于之前的几种方法，收敛的速度快得多，前面的几种方法次数动辄十几次几十次，而Newton-Raphson方法一般来说只需要不到十次，而且相对真值的误差减小速度远远快于近似相对误差的减小速度。是一种较优的求根方法。

6.割线法

割线法一方面类似于Newton-Raphson方法，但其不同点是用差分估计斜率。另一方面类似于试位法，都是使用两个初值来计算函数斜率的近似，并将其投射到x轴上获得一个新的估计值。其迭代公式为：

x i+1=x i?f(x i)

x i?x i?1

f(x i)?f(x i?1)

源代码secant.m（函数定义）：

function [p1,c,ea,es,y]=secant(p0,p1,tol,epsilon) %input - p0,p1 is the initial guess for the zero

% - tol is the tolerance between the guessed zeros % - epsilon is the tolerance of y and 0

%output - p1 is the zero

% - y=f(p1)

% - c is the times of iteration

% - ea is the error in the approximation

% - es is the error between the true value

f=@(x)(-5*x^4+2*600^2*3*x^2-600^4);

y=f(p1);

p1n=p1; %last estimated zero

c=0;

while (abs(p1-p0)>tol && abs(y)>epsilon)

c=c+1;

p2=p1-f(p1)*(p1-p0)/(f(p1)-f(p0));

p0=p1;

p1=p2;

ea=abs((p1-p1n)/p1);

p1n=p1; %update zero

es=abs((p1-600)/600); %the first root

%es=abs((p1-268.328157299975)/268.328157299975);%second root

fprintf('root=%g ea=%g es=%g\n',p1,ea,es);

y=f(p1);

end

p1=vpa(p1,15);

表6.割线法计算结果

6 200 300 1e-3 1e-3 4 268.3281572 2.4723e-11 6.3553e-16 4.5776e-05

由迭代过程可以看出，割线法收敛到真实根的速度也较快，而且相对真实根的误差减小

速度远远快于近似相对误差的减小速度。相比于Newton-Raphson方法，由于割线法通过两

个参数来确定割线位置，所以可以避免Newton-Raphson方法中除数为0的缺点。而且初始

给定的两个估计参数不用像二分法或者试位法一样，需要界定根的位置。所以割线法是一个

较优的方法。

7. 改进的Newton-Raphson方法和改进的割线法

针对出现重根的情况，原本2阶或接近2阶的收敛速率会下降到线性收敛速率，改进方法如下：

定义一个新函数：

u(x)=

f(x)

此函数与原函数有相同的根。基于此函数得到：

改进的Newton-Raphson方法：

x i+1=x i?

f(x i)f′(x i) (i)2(i)(i)

改进的割线法：

x i+1=x i?u(x i)

x i?x i?1 (i)i?1

原理和迭代方法并没有变化。由于本题并未出现重根的状况以及时间方面的原因，所以此处未进行编程验证。

四．总结

表7.各种方法特点的总结

试位法不会发散停滞的划界点会影响效率、

收敛速度不够快

能发散、每个g(x)只对应一个

割线法收敛速度快、划界无需知道

根的范围

可能会发散

非线性方程求根方法比较多，所适用的条件和范围也不尽相同。我们在实际应用的时候，需要根据情况，选择最优的解决方案。