FFT函数介绍

matlab的FFT函数
2010-04-26 22:16
相关语法:
Y = fft(X)
Y = fft(X,n)
Y = fft(X,[],dim)
Y = fft(X,n,dim)
定义如下:
相关的一个例子:
Fs = 1000; % 采样频率
T = 1/Fs; % 采样时间
L = 1000; % 总的采样点数
t = (0:L-1)*T; % 时间序列(时间轴)
%产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz 的正弦信号
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
y = x + 2*randn(size(t)); % 混入噪声信号
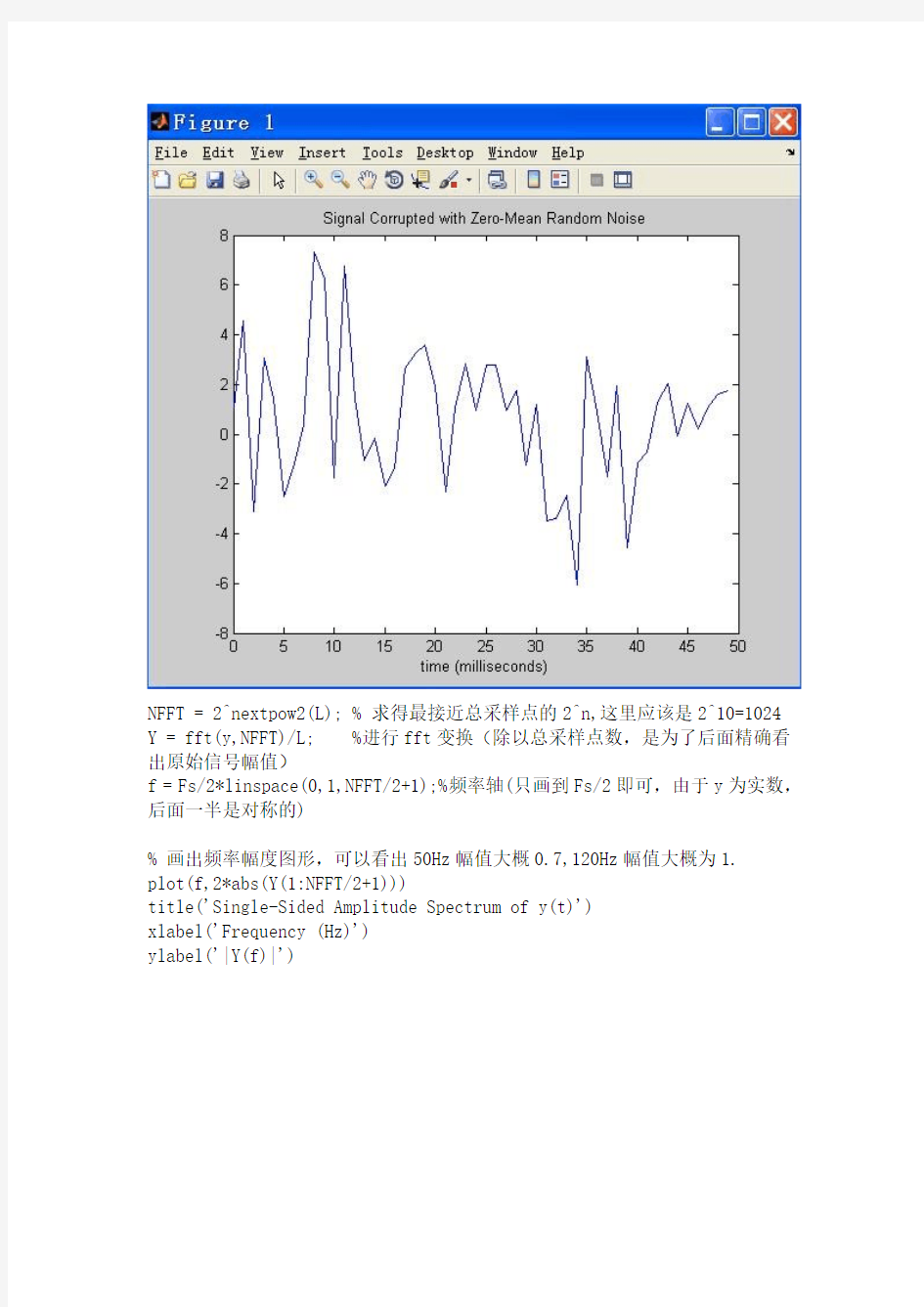
plot(Fs*t(1:50),y(1:50)) %画出前50个点
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')
NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值)
f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的)
% 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1.
plot(f,2*abs(Y(1:NFFT/2+1)))
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
PS:前段时间,只是为了自己看明白,没有管太多,刚才上空间发现几位的留言,感觉惭愧。其实要掌握matlab中fft的用法,
主要有两点注意的地方:
1、从公式上看,matlab的fft序号是从1到N,但是绝大多数教材上是从0到N-1。
2、Y=fft(x)之后,这个Y是一个复数,它的模值应该除以(length(x)2),才能得到各个频率信号实际幅值。
Matlab编程实现FFT变换.
Matlab编程实现FFT变换及频谱分析的程序代码 内容 1.用Matlab产生正弦波,矩形波,以及白噪声信号,并显示各自时域波形图 2.进行FFT变换,显示各自频谱图,其中采样率,频率、数据长度自选 3.做出上述三种信号的均方根图谱,功率图谱,以及对数均方根图谱 4.用IFFT傅立叶反变换恢复信号,并显示恢复的正弦信号时域波形图 源程序 %*************************************************************** **********% % FFT实践及频谱分析% %*************************************************************** **********% %*************************************************************** **********% %***************1.正弦波****************% fs=100;%设定采样频率 N=128; n=0:N-1; t=n/fs; f0=10;%设定正弦信号频率 %生成正弦信号 x=sin(2*pi*f0*t); figure(1); subplot(231); plot(t,x);%作正弦信号的时域波形 xlabel('t'); ylabel('y'); title('正弦信号y=2*pi*10t时域波形'); grid; %进行FFT变换并做频谱图 y=fft(x,N);%进行fft变换 mag=abs(y);%求幅值 f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换 figure(1); subplot(232); plot(f,mag);%做频谱图 axis([0,100,0,80]); xlabel('频率(Hz)'); ylabel('幅值'); title('正弦信号y=2*pi*10t幅频谱图N=128'); grid; %求均方根谱
matlab的FFT函数
matlab的FFT函数 相关语法: Y = fft(X) Y = fft(X,n) Y = fft(X,[],dim) Y = fft(X,n,dim) 定义如下: 相关的一个例子: Fs = 1000; % 采样频率 T = 1/Fs; % 采样时间 L = 1000; % 总的采样点数 t = (0:L-1)*T; % 时间序列(时间轴) %产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz 的正弦信号 x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); y = x + 2*randn(size(t)); % 混入噪声信号 plot(Fs*t(1:50),y(1:50)) %画出前50个点 title('Signal Corrupted with Zero-Mean Random Noise') xlabel('time (milliseconds)')
NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值) f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的) % 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1. plot(f,2*abs(Y(1:NFFT/2+1))) title('Single-Sided Amplitude Spectrum of y(t)') xlabel('Frequency (Hz)') ylabel('|Y(f)|')
MATLAB中的FFT实例讲解
MATLAB仿真实验 傅里叶变换与信号频谱图 本实验将简要介绍如何利用FFT函数描绘指定信号的频谱图像。 一、相关函数 1、FFT函数 离散傅里叶(Fourier)变换函数。 【语法】 Y = fft(X) Y = fft(X,n) Y = fft(X,[],dim) Y = fft(X,n,dim) 相关函数:IFFT(x)逆傅里叶变换。 【例1】画出函数y(t)的图像。 t = 0:0.001:0.6; x = sin(2*pi*50*t)+sin(2*pi*120*t); y = x + 2*randn(size(t)); plot(1000*t(1:50),y(1:50)) title('Signal Corrupted with Zero-Mean Random Noise') xlabel('time (milliseconds)')
Signal Corrupted with Zero-Mean Random Noise Frequency content of y
【图像】
Power spectral density Frequency (Hz)(a)时域图f(t)(b)频域图F(ω) 图3Sin(100πt)+2Sin(280πt)的频谱图
4、()(100)(280)f t Sin t Cos t ππ=g 的频谱图 调制信号sin(100)t π,载波cos(280)t π。 【程序】 Frequency (Hz) Frequency (Hz) 图(c )Cos (280πt )频谱图 图4 Sin (100πt )Cos (280πt )的频谱图
Matlab中的FFT使用说明
FFT是Fast Fourier Transform(快速傅里叶变换)的简称,FFT算法在MATLAB 中实现的函数是Y=fft(x,n)。刚接触频谱分析用到FFT时,几乎都会对MATLAB 的fft函数产生一些疑惑,下面以看一个例子(根据MATLA帮助修改)。 Fs = 2000; % 设置采样频率 T = 1/Fs; % 得到采用时间 L = 1000; % 设置信号点数,长度1 秒 t = (0:L-1)*T; % 计算离散时间, % 两个正弦波叠加 f1 = 80; A1 = 0.5; % 第一个正弦波100Hz,幅度0.5 f2 = 150; A2 = 1.0 ; % 第2个正弦波150Hz,幅度 1.0 A3 = 0.5; % 白噪声幅度; x = A1*sin(2*pi*f1*t) + A2*sin(2*pi*f2*t); % 产生离散时间信号; y = x + A3*randn(size(t)); % 叠加噪声; % 时域波形图 subplot(2,1,1) plot(Fs*t(1:50),x(1:50)) title('Sinusoids Signal') xlabel('time (milliseconds)') subplot(2,1,2) plot(Fs*t(1:50),y(1:50)) title('Signal Corrupted with Zero-Mean Random Noise') xlabel('time (milliseconds)') NFFT = 2A nextpow2(L); % 设置FFT点数,一般为2 的N次方,如1024,512 等Y = fft(y,NFFT)/L; % 计算频域信号, f = Fs/2*linspace(0,1,NFFT/2+1); %频率离散化,fft后对应的频率是-Fs/2到Fs/2,由NFFT个离散频点表示 % 这里只画出正频率; % Plot single-sided amplitude spectrum. figure; plot(f,2*abs(Y(1:NFFT/2+1))); % fft 后含幅度和相位,一般观察幅度谱,并把负频率加上去, title('Single-Sided Amplitude Spectrum of y(t)') xlabel('Frequency (Hz)')
FFT实现自相关函数
FFT实现自相关函数 N=38; noise=(randn(1,N)+1i*randn(1,N))/sqrt(2); f1=0.11; f2=0.15; f3=0.23; SNR1=20; SNR2=18; SNR3=17; A1=10^(SNR1/20); A2=10^(SNR2/20); A3=10^(SNR3/20); signal1=A1*exp(1i*2*pi*f1*(0:N-1)); signal2=A2*exp(1i*2*pi*f2*(0:N-1)); signal3=A3*exp(1i*2*pi*f3*(0:N-1)); un=signal1+signal2+signal3+noise; Uk=fft(un,2*N); Sk=(1/N)*abs(Uk).^2;r0=ifft(Sk); r1=[r0(N+2:2*N),r0(1:N)]; r=xcorr(un,N-1,'biased'); r11=real(r1); r12=imag(r1); r1=real(r); r2=imag(r); m=1-N:N-1; subplot(2,2,1); stem(m,r11,'o'); xlabel('m'); ylabel('实部'); title('基于FFT的自相关函数'); subplot(2,2,2); stem(m,r12,'o'); xlabel('m'); ylabel('虚部'); subplot(2,2,3); stem(m,r1); xlabel('m'); ylabel('实部');
title('基于直接计算的自相关函数'); subplot(2,2,4); stem(m,r2); xlabel('m'); ylabel('虚部');
MATLAB中FFT的使用方法
MATLAB中FFT的使用方法 一.调用方法 X=FFT(x); X=FFT(x,N); x=IFFT(X); x=IFFT(X,N) 用MATLAB进行谱分析时注意: (1)函数FFT返回值的数据结构具有对称性。 例: N=8; n=0:N-1; xn=[4 3 2 6 7 8 9 0]; Xk=fft(xn) →Xk = 39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0。 (2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。 二.FFT应用举例 例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。 clf; fs=100;N=128; %采样频率和数据点数
n=0:N-1;t=n/fs; %时间序列 x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求得Fourier变换后的振幅 f=n*fs/N; %频率序列 subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; %对信号采样数据为1024点的处理 fs=100;N=1024;n=0:N-1;t=n/fs; x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求取Fourier变换的振幅 f=n*fs/N; subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; subplot(2,2,4) plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; 运行结果:
FFT超全快速傅里叶
快速傅里叶变换 FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。 虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。 现在圈圈就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号,经过ADC采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。 采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。 假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。而每个点的相位呢,就是在该频率下的信号的相位。第一个表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示 采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。例如某点n所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。如果要提高
关于使用Matlab里Powergui的FFTTool分析的问题及解决办法
首先设置 POWERLIB—》powergui,将该模块拖入模型中即可 在需要进行频谱分析的地方连接一示波器 示波器参数设定: Parameters—》Data history—》Save data to workspace; Format—》Structure with time. 运行一次后,双击powergui—》FFT Analysis. 1. 问题1及解决办法 仿真完成后,采用Powergui分析FFT,有时会发生错误:"simulation time of the signals is not enough long for the given fundamental frequency". 很多论坛说是仿真时间短了,可能这也是原因,不过更有可能是这样: FFT的数据来自于示波器SCOPE,在SCOPE PARAMETERS/GENERAL选项卡/SAMPLING 中,有DECIMATION和SAMPLE TIME两项,DECIMATION的意思是 The Decimation parameter allows you to write data at every nth sample, where n is the decimation factor. The default decimation, 1, writes data at every time step. 所以,如果选择DECIMATION,记录数据的时刻为第N个采样点,采样点间的时间间隔为采样步长,而在MATLAB Simulink中,如果采用变步长仿真,采样周期就是变化的,这样就很难对采样的数据进行FFT分析,或许软件只认可采样周期一定的数据,所以会出现文首的错误。 如果选择sample time,那么采样周期固定(与仿真步长无关),这样就可以进行FFT 分析了。所以如果遇到文首的错误,可以尝试将示波器的SAMPLing改为sample time,并设定采样周期,Sampling time
matlab的FFT函数介绍
matlab的FFT函数 2010-04-26 22:16 相关语法: Y = fft(X) Y = fft(X,n) Y = fft(X,[],dim) Y = fft(X,n,dim) 定义如下: 相关的一个例子: Fs = 1000; % 采样频率 T = 1/Fs; % 采样时间 L = 1000; % 总的采样点数 t = (0:L-1)*T; % 时间序列(时间轴) %产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz 的正弦信号 x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); y = x + 2*randn(size(t)); % 混入噪声信号 plot(Fs*t(1:50),y(1:50)) %画出前50个点 title('Signal Corrupted with Zero-Mean Random Noise') xlabel('time (milliseconds)')
NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值) f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的) % 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1. plot(f,2*abs(Y(1:NFFT/2+1))) title('Single-Sided Amplitude Spectrum of y(t)') xlabel('Frequency (Hz)') ylabel('|Y(f)|')
MATLAB中FFT使用详解
MATLAB中FFT使用详解 一.调用方法 X=FFT(x); X=FFT(x,N); x=IFFT(X); x=IFFT(X,N) 用MA TLAB进行谱分析时注意: (1)函数FFT返回值的数据结构具有对称性。 例: N=8; n=0:N-1; xn=[4 3 2 6 7 8 9 0]; Xk=fft(xn) → Xk = 39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0。 (2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。 二.FFT应用举例 例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。 clf; fs=100;N=128; %采样频率和数据点数 n=0:N-1;t=n/fs; %时间序列 x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求得Fourier变换后的振幅 f=n*fs/N; %频率序列 subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; %对信号采样数据为1024点的处理 fs=100;N=1024;n=0:N-1;t=n/fs; x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求取Fourier变换的振幅 f=n*fs/N; subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; subplot(2,2,4) plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; 运行结果: fs=100Hz,Nyquist频率为fs/2=50Hz。整个频谱图是以Nyquist频率为对称轴的。并且可以明显识别出信号中含有两种频率成分:15Hz和40Hz。由此可以知道FFT变换数据的对称性。因此用FFT对信号做谱分析,只需考察0~Nyquist频率范围内的福频特性。若没有给出采样频率和采样间隔,则分析通常对归一化频率0~1进行。另外,振幅的大小与所用采样点数有关,采用128点和1024点的相同频率的振幅是有不同的表现值,但在同一幅图中,40Hz
MATLAB中FFT函数理解
MATLAB中FFT函数理解 2010-09-06 12:15 matlab的FFT函数 相关语法: Y = fft(X) Y = fft(X,n) Y = fft(X,[],dim) Y = fft(X,n,dim) 定义如下: 相关的一个例子: Fs = 1000; % 采样频率 T = 1/Fs; % 采样时间 L = 1000; % 总的采样点数 t = (0:L-1)*T; % 时间序列(时间轴) %产生一个幅值为0.7频率为50HZ正弦+另外一个信号的幅值为1频率为120Hz的正弦信号 x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); y = x + 2*randn(size(t)); % 混入噪声信号 plot(Fs*t(1:50),y(1:50)) %画出前50个点 title('Signal Corrupted with Zero-Mean Random Noise') xlabel('time (milliseconds)')
NFFT = 2^nextpow2(L); % 求得最接近总采样点的2^n,这里应该是2^10=1024 Y = fft(y,NFFT)/L; %进行fft变换(除以总采样点数,是为了后面精确看出原始信号幅值) f = Fs/2*linspace(0,1,NFFT/2+1);%频率轴(只画到Fs/2即可,由于y为实数,后面一半是对称的) % 画出频率幅度图形,可以看出50Hz幅值大概0.7,120Hz幅值大概为1. plot(f,2*abs(Y(1:NFFT/2+1))) title('Single-Sided Amplitude Spectrum of y(t)') xlabel('Frequency (Hz)') ylabel('|Y(f)|')
MATLAB中FFT的使用方法
MATLAB中FFT的使用方法 调用方法 X=FFT(x); X=FFT(x,N);%N为FFT后的数据点数,如果实际信号的数据点数小于N的话,则需要在FFT变换时增加采样点数,或者通过采用频率细分法在原数据后面补充一定数量的0,从而满足N个数据点 X=IFFT(X); X=IFFT(X,N) 一、用MATLAB进行谱分析时注意: (1)函数FFT返回值的数据结构具有对称性。 例: N=8; n=0:N-1; xn=[4 3 2 6 7 8 9 0]; Xk=fft(xn) Xk = 39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0。 (2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。
在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。 二、FFT应用举例 例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。 clf; fs=100;N=128; %采样频率和数据点数 n=0:N-1;t=n/fs; %时间序列 x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求得Fourier变换后的振幅 f=n*fs/N; %频率序列 subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; %对信号采样数据为1024点的处理 fs=100; N=1024;
数字信号处理 实验一 FFT变换及其应用
实验一 FFT变换及其应用 一、实验目的和要求 1.在理论课学习的基础上,通过本次实验,加深对DFT原理的理解,懂得 频域DFT与时域卷积的关系,进一步加深对DFT基本性质的理解; 2.研究FFT算法的主要途径和编程思路,掌握FFT算法及其程序的编写过程, 掌握最基本的时域基-2FFT算法原理及程序框图; 3.熟悉应用FFT实现两个序列的线性卷积的方法,利用FFT进行卷积,通过 实验比较出快速卷积优越性,掌握循环卷积和线性卷积两者之间的关系; 4.熟悉应用FFT对典型信号进行频谱分析的方法,初步了解用周期图法作随 机信号谱分析的方法,了解应用FFT进行信号频谱分析过程中可能出现的 问题,以便在实际中正确应用FFT; 5.掌握使用MATLAB等基本开发工具实现对FFT编程。 二、实验设备和分组 1.每人一台PC机; 2.Windows 2000/XP以上版本的操作环境; 3.MatLab 6.5及以上版本的开发软件。 三、实验内容 (一)实验准备 1.用FFT进行谱分析涉及的基础知识如下: 信号的谱分析就是计算信号的傅里叶变换。若信号是模拟信号,用FFT进行谱分析时,首先必须对信号进行采样,使之变成离散信号,然后用FFT来对连续信号进行谱分析。 若信号本身是有限长的序列,计算序列的频谱就是直接对序列进行FFT运算求得X(k),X(k)就代表了序列在[0,2]之间的频谱值。 幅度谱: 相位谱:
为避免产生混叠现象,采样频率fs 应大于2倍信号的最高频率fc ,为了满足采样定理,一般在采样之前要设置一个抗混叠低通滤波器。 用FFT 对模拟信号进行谱分析的方框图如下所示。 图1.1 FFT 对模拟信号进行谱分析的方框图 2. 应用FFT 实现快速卷积涉及的基础知识如下: 一个信号序列x(n)与系统的卷积可表示为下式: Y(n)=x(n)*h(n)= ∑+∞ -∞ =-m m n h m x )()( 当是一个有限长序列,且0≤n ≤N-1时,有: Y(n)= ∑-=-1 )()(N n m n x m h 此时就可以应用FFT 来快速计算有限长度序列的线性卷积。 也就是先将输入信号x (n )通过FFT 变换为它的频谱采样值X(k),然后再和滤波器的频响采样值H(k)相乘,最后再将乘积通过快速傅里叶变换(简称IFFT )还原为时域序列,即得到输出。如下图所示。 图1.2 FFT 实现卷积的过程示意图 2.1.当序列x(n)和h(n)的长度差不多时 设x(n)的长度为N1,h(n)的长度为N2,则用FFT 完成卷积的具体步骤如下: ①为使两有限长序列的线性卷积可用其循环卷积代替而不发生混叠,必须选择循环卷积长度N ≥N1+N2-1 ②用补零方法使x(n)和h(n)变成列长为N 的序列。 ③用FFT 计算x(n)和h(n)的N 点离散傅里叶变换 ④完成X(k)和H(k)的乘积Y(k)。
利用MATLAB编写FFT快速傅里叶变换
一、实验目的 1.利用MATLAB 编写FFT 快速傅里叶变换。 2.比较编写的myfft 程序运算结果与MATLAB 中的FFT 的有无误差。 二、实验条件 PC 机,MATLAB7.0 三、实验原理 1. FFT (快速傅里叶变换)原理: 将一个N 点的计算分解为两个N/2点的计算,每个N/2点的计算再进一步分解为N/4点的计算,以此类推。根据DFT 的定义式,将信号x[n]根据采样号n 分解为偶采样点和奇采样点。设偶采样序列为y[n]=x[2n],奇采样序列为z[n]=x[2n+1]。 上式中的k N W -为旋转因子N k j e /2π-。下式则为y[n]与z[n]的表达式: 2. 蝶形变换的原理:
下图给出了蝶形变换的运算流图,可由两个N/2点的FFT (Y[k]和Z[k]得出N 点FFT X[k])。同理,每个N/2点的FFT 可以由两个N/4点的FFT 求得。按这种方法,该过程可延迟后推到2点的FFT 。 下图为N=8的分解过程。图中最右边的为8个时域采样点的8点FFTX[k],由偶编号采样点的4点FFT 和奇编号采样点的4点得到。这4点偶编号又由偶编号的偶采样点的2点FFT 和奇编号的偶采样点的2点FFT 产生。相同的4点奇编号也是如此。依次往左都可以用相同的方法算出,最后由偶编号的奇采样点和奇编号的偶采样点的2点FFT 算出。图中没2点FFT 成为蝶形,第一级需要每组一个蝶形的4组,第二级有每组两个蝶形的两组,最后一级需要一组4个蝶形。 四、实验内容 1.定义函数disbutterfly ,程序根据FFT 的定义:]2 [][][N n x n x n y + +=、n N W N n x n x n z -+ -=])2 [][(][,将序列x 分解为偶采样点y 和奇采样点z 。
FFT的前世今生(三)窗函数的选择
力科示波器基础应用系列之八 FFT的前世今生(三) Teledyne LeCroy 马亦飞 窗函数对于FFT结果的影响 所谓频谱泄露,就是信号频谱中各谱线之间相互干扰,使测量的结果偏离实际值,同时在真实谱线的两侧的其它频率点上出现一些幅值较小的假谱。产生频谱泄露的主要原因是采样频率和原始信号频率不同步,造成周期的采样信号的相位在始端和终端不连续。简单来说就是因为计算机的FFT 运算能力有限,只能处理有限点数的FFT,所以在截取时域的周期信号时,没有能够截取整数倍的周期。信号分析时不可能取无限大的样本。只要有截断不同步就会有泄露。 在图1和图2中,为了最大化FFT运算之后的频率分辨率,我们使用了矩形窗。图中的时域信号是500MHz正弦波信号,在频谱上应该仅在500MHz频点上看到谱线。FFT运算研究的是整个时间域(-∞,+∞)与频域的关系,所以对于矩形窗函数截取的波形应该认为是无穷延续的,因此,矩形窗100ns时间窗内,包含了500MHz正弦波整50个周期,所以波形的首尾能够整周期得无缝连接,FFT之后的频谱会在500MHz频点看到较为纯净的能量值。如下图1所示: 图1:矩形时间窗口内包含整数倍周期的信号,首尾可以“无缝”连接 事实上,大多数类型的信号都不满足上面的这种特殊情况,绝大多数信号在时间窗口内都不是整周期的倍数,在这种情况下,FFT之后的频谱就不能看做连续的正弦波了。例如,如果该正弦波的频率是495MHz,在100ns时间窗口内包含49.5个周期,因此在截取窗口的首尾部分就存在很大程度上的“不连续”,这种“不连续”会直接影响FFT之后的结果。“不连续”部分的能量会散落在整个频谱范围内,使用100ns时间窗口,FFT之后的频率分辨率是10MHz,495MHz频点即落在490MHz与500MHz之间,所以495MHz正弦波信号的能量分成两部分,所以从频谱上看,峰值谱线明显降低了,这被称作是频谱泄露
MATLAB中FFT的使用方法
MATLAB FFT 的使用方法 2009-08-22 11:00 说明:以下资源来源于《数字信号处理的 MATLAB ;现》万永革主编 一.调用方法 X=FFT(X); X=FFTX, N); x=IFFT(X); x=IFFT(X,N) 用MATLAB!行谱分析时注意: (1) 函数FFT 返回值的数据结构具有对称性。 例: N=8; n=0:N-1; xn=[4 3 2 6 7 8 9 0]; Xk=fft(xn) Xk = -10.7782 + 6.2929i 7.7071i 5.0000 0 + 5.0000i -10.7782 - 6.2929i Xk 与xn 的维数相同,共有8个元素。Xk 的第一个数对应于直流分量,即频率值 为00 (2) 做FFT 分析时,幅值大小与FFT 选择的点数有关,但不影响分析结果。在 IFFT 时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果 乘以2除以N 即可。 二.FFT 应用举例 例 1: x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t) 。采样频率 fs=100Hz,分别绘 制N=128 1024点幅频图。 clf; fs=100;N=128; %采样频率和数据点数 n=0:N-1;t=n/fs; %时间序歹 U x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); % 信号 39.0000 5.0000i 4.7782 + 7.7071i 4.7782
y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求得Fourier变换后的振幅 f=n*fs/N; %? 率序列 subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; subplot(2,2,2),plot(f(1:N⑵,mag(1:N⑵);%绘出Nyquist 频率之前随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; 以对信号采样数据为1024点的处理 fs=100;N=1024;n=0:N-1;t=n/fs; x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); % 信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求取Fourier变换的振幅 f=n*fs/N; subplot(2,2,3),plot(f,mag); % 绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; subplot(2,2,4) plot(f(1:N/2),mag(1:N/2)); % 绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; 运行结果:
关于DSP中fft函数调用方法
关于DSP中fft函数调用方法 以下主要是通过代码调用fft函数 1、通过dsplib库调用DSPF_sp_ifftSPxSP函数来实现fft //fft tw_gen_fft (w_array,N); DSPF_sp_fftSPxSP (N,x_array,w_array,y_array,brev,rad,0,N); 其中函数tw_gen_fft()为旋转因子,计算大码为: void tw_gen_ifft (float *w,int n) { int i,j,k; const double PI = 3.141592654; for (j = 1,k = 0; j 《= n 》》2; j = j 《《2) { for (i = 0; i 《n 》》2; i += j) { #ifdef _LITTLE_ENDIAN w[k]= (float)-sin (2 * PI * i / n);//为负数的时候是进行IFFT,为正数的时候是进行FFT w[k + 1]= (float)cos (2 * PI * i / n); w[k + 2]= (float)-sin (4 * PI * i / n); w[k + 3]= (float)cos (4 * PI * i / n); w[k + 4]= (float)-sin (6 * PI * i / n); w[k + 5]= (float)cos (6 * PI * i / n); #else w[k]= (float)cos (2 * PI * i / n); w[k + 1]= (float)-sin (2 * PI * i / n);
MATLAB中FFT的使用方法(频谱分析)
说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编 一.调用方法 X=FFT(x); X=FFT(x,N); x=IFFT(X); x=IFFT(X,N) 用MATLAB进行谱分析时注意: (1)函数FFT返回值的数据结构具有对称性。 例: N=8; n=0:N-1; xn=[4 3 2 6 7 8 9 0]; Xk=fft(xn) → Xk = 39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0。 (2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。 二.FFT应用举例 例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。 clf; fs=100;N=128; %采样频率和数据点数
n=0:N-1;t=n/fs; %时间序列 x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求得Fourier变换后的振幅 f=n*fs/N; %频率序列 subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅xlabel('频率/Hz'); ylabel('振幅');title('N=128');grid on; %对信号采样数据为1024点的处理 fs=100;N=1024;n=0:N-1;t=n/fs; x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求取Fourier变换的振幅 f=n*fs/N; subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on; subplot(2,2,4) plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅 xlabel('频率/Hz'); ylabel('振幅');title('N=1024');grid on;
MATLAB中FFT的运用方法
MATLAB中FFT的使用方法 说明:以下资源来源于《数字信号处理的MATLAB实现》万永革主编 一.调用方法 X=FFT(x); X=FFT(x,N); x=IFFT(X); x=IFFT(X,N) 用MATLAB进行谱分析时注意: (1)函数FFT返回值的数据结构具有对称性。 例: N=8; n=0:N-1; xn=[4 3 2 6 7 8 9 0]; Xk=fft(xn) → Xk = 39.0000 -10.7782 + 6.2929i 0 - 5.0000i 4.7782 - 7.7071i 5.0000 4.7782 + 7.7071i 0 + 5.0000i -10.7782 - 6.2929i Xk与xn的维数相同,共有8个元素。Xk的第一个数对应于直流分量,即频率值为0。 (2)做FFT分析时,幅值大小与FFT选择的点数有关,但不影响分析结果。在IFFT时已经做了处理。要得到真实的振幅值的大小,只要将得到的变换后结果乘以2除以N即可。 二.FFT应用举例 例1:x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)。采样频率fs=100Hz,分别绘制N=128、1024点幅频图。 clf; fs=100;N=128; %采样频率和数据点数 n=0:N-1;t=n/fs; %时间序列 x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号 y=fft(x,N); %对信号进行快速Fourier变换 mag=abs(y); %求得Fourier变换后的振幅 f=n*fs/N; %频率序列 subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅
