四边形之存在性问题(二)(讲义及答案)

四边形之存在性问题(二)(讲义)
?课前预习
1.一般情况下我们如何处理存在性问题?
(1)研究背景图形
坐标系背景下研究____________、____________;几何图形研究____________、____________、____________.
(2)根据不变特征,确定分类标准
研究定点,动点,定线段,确定分类标准
不变特征举例:
①等腰三角形(两定一动)
以定线段作为_________或者___________来分类,利用
_______________确定点的位置.
②等腰直角三角形(两定一动)
以________________来分类,然后借助_________或者
___________确定点的位置.
(3)分析特殊状态的形成因素,画出符合题意的图形并求解
(4)结果验证
2.用铅笔做讲义第1,2题,并将计算、演草保留在讲义上,先看知识点睛,再做
题,思路受阻时(某个点做了2~3分钟)重复上述动作,若仍无法解决,课堂重点听.
?知识点睛
1.存在性问题处理框架:
①研究背景图形;
②根据不变特征,确定分类标准;
③分析特殊状态的形成因素,画出符合题意的图形并求解;
④结果验证.
2.特殊平行四边形存在性问题不变特征举例:
①菱形存在性问题(两定两动)
转化为等腰三角形存在性问题;
以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,然后通过平移确定另一动点坐标.
②正方形存在性问题(两定两动)
转化为等腰直角三角形存在性问题;
根据直角顶点确定分类标准,利用两腰相等或者45°角确定一动点的位置,然后通过平移确定另一动点坐标.
?精讲精练
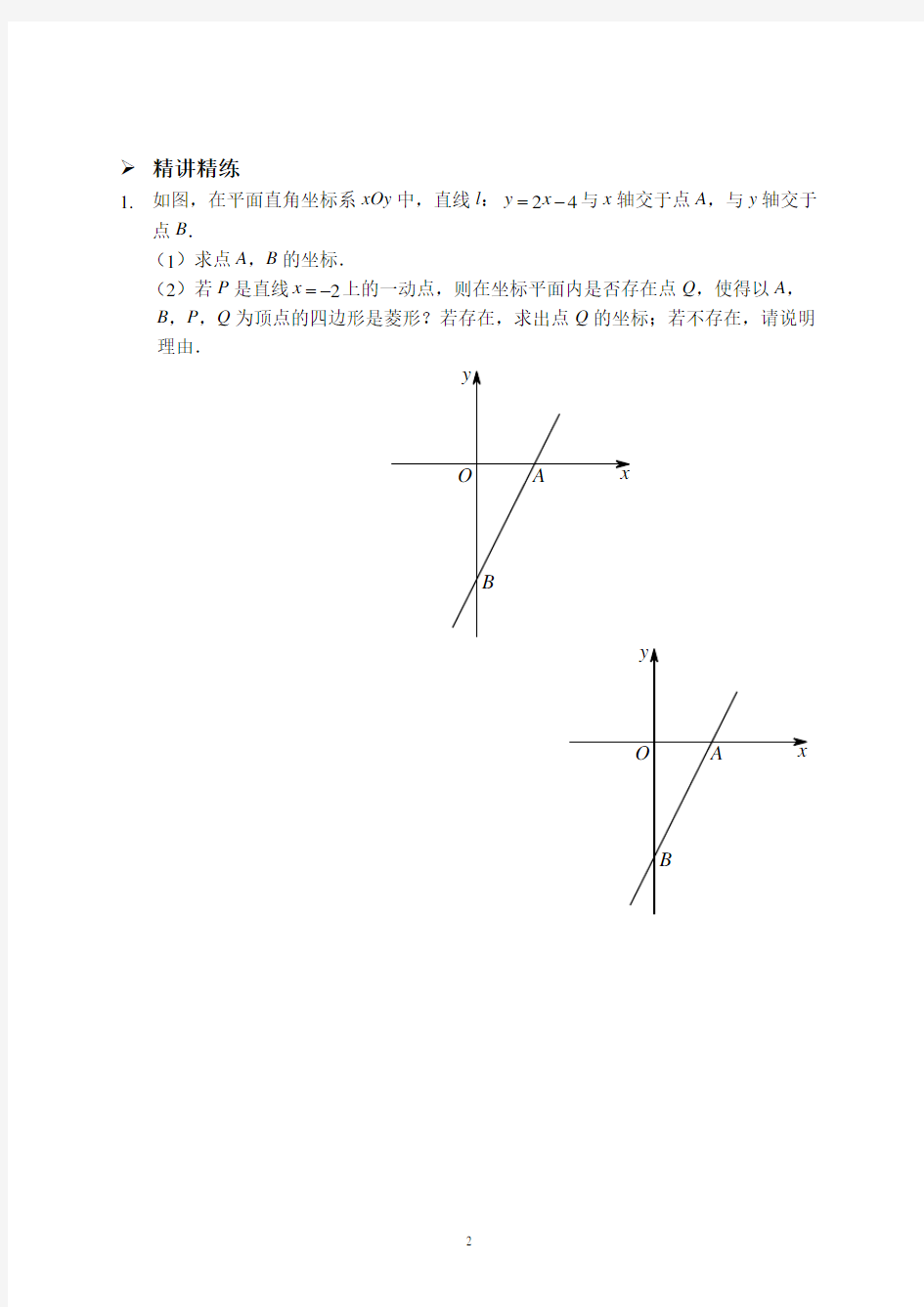
1.如图,在平面直角坐标系xOy中,直线l:24
=-与x轴交于点A,与y轴交于
y x
点B.
(1)求点A,B的坐标.
(2)若P是直线2
x=-上的一动点,则在坐标平面内是否存在点Q,使得以A,B,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系xOy中,直角梯形
点C的坐标为(18
,0),A B∥O C,
∠OCB=45°,且BC
=
(1)求点B的坐标.
(2)直线BE与线段OA交于点E,且OE=6.若P是直线BE上的一动点,则在坐标平面内是否存在点Q,使得以O,E,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
3.
为坐标平面内一点,则在第一象限内是否存在点F ,使得以A ,C ,F ,M 为顶点的四边形是正方形?若存在,求出点F 的坐标;若不存在,请说明理由.
4.如图,在平面直角坐标系中,已知点A,B,C的坐标分别为A(9 ,0),B(16,
0),C(0,12),D是线段BC上的一动点(不与点B,C重合),过点D作直线DE
⊥OB,垂足为点E.若M为坐标平面内一点,则在直线DE上是否存在点N,使得以C,B,M,N为顶点的四边形是正方形?若存在,求出点N的坐标;若不存在,请说明理由.
【参考答案】 ? 课前预习
1.(1)坐标;表达式;边;角;形 (2)①腰;底;两圆一线
②直角顶点;两腰相等;45°角 ? 精讲精练
1.(1)A (2,0),B (0,-4);
(2)存在;点Q 的坐标为(0,4),(-4,-2),(-4,-6)或(4,72
-).
2.(1)B (-6,12);
(2)存在,点Q 的坐标为(6,6),(-,(-或(3-,3).
3.存在,点F 的坐标为(3,3,(3+)或(
32+,32
+). 4.存在,点N 的坐标为(12,28),(4,16-),(14,14)或(2,2-).
平行四边形的存在性问题
平行四边形的存在性问题 【真题典藏】 1.(2008年青浦区第24题)如图1,在平面直角坐标系中,点O 是坐标原点,正比例函数kx y =(x 为自变量)的图像与双曲线x y 2 - =交于点A ,且点A 的横坐标为2-. (1)求k 的值. (2)将直线kx y =(x 为自变量)向上平移4个单位得到直线BC ,直线BC 分别交x 轴、y 轴于B 、 C ,如点 D 在直线BC 上,在平面直角坐标系中求一点P ,使以O 、B 、D 、P 为顶点的四边形是菱形. 图1 图2 2.(2009年普陀区第25题)如图2,在平面直角坐标系xOy 中,O 为原点,点A 、C 的坐标分别为(2, 0)、(1,33). 将△AOC 绕AC 的中点旋转180°,点O 落到点B 的位置,抛物线x ax y 322 -=经 过点A ,点D 是该抛物线的顶点. (1)求证:四边形ABCO 是平行四边形; (2)求a 的值并说明点B 在抛物线上; (3)若点P 是线段OA 上一点,且∠APD =∠OAB ,求点P 的坐标; (4)若点P 是x 轴上一点,以P 、A 、D 为顶点作平行四边形,该平行四边形的另一顶点在y 轴上,写出点P 的坐标. 3.(2010年上海市第24题)参见《考典40 几何计算说理与说理计算问题》第3题. 4.(2011年上海市第24题)已知平面直角坐标系xOy (如图3),一次函数3 34 y x =+的图像与y 轴交于点A ,点M 在正比例函数3 2 y x = 的图像上,且MO =MA .二次函数 y =x 2+bx +c 的图像经过点A 、M . (1)求线段AM 的长; (2)求这个二次函数的解析式;
实验 平行四边形定则
实验三 验证力的平行四边形定则 一、实验目的: 探究力的合成规律 —— 平行四边形定则;理解等效替代思想方法在物理学中的应用. 二、实验原理: 互成角度的两个力与一个力产生 相同 的效果,看它们用平行四边形定则求出的合力与这个力是否在实验误差允许的范围内相等. 三、实验器材: 木板、白纸、图钉若干、 橡皮条 、细绳、弹簧秤(2只)、三角板、 刻度尺 ,等. 四、实验步骤: ① 用图钉把一张白纸钉在水平桌面上的 方木板 上,如图所示; ②用两个弹簧秤分别钩住两个绳套,互成角度地拉橡皮条,使橡皮条伸长, 结点到达某一点O ; ③用铅笔描下 结点O 的 位置和两个细绳套的 方向 ,并记录弹簧秤的读数21F F ,利用刻度尺和三角板作平行边形,画出对角线所代表的力F ; ④只用一个弹簧秤,通过细绳套把橡皮条的结点拉到与前面实验中的相同 位置O ,记下弹簧的读数F ′ 和细绳的方向; ⑤比较F 和F ′,观察它们在实验误差允许的范围内是否 相等 . ⑥改变21F F ,的大小和方向,再做两次实验。 五、误差分析: 实验误差除弹簧测力计本身的误差外,还主要来源于 读数 误差和 作图 误差两个方面.
① 减小读数误差的方法:弹簧测力计数据在允许的情况下,尽量 大 一些.读数时眼睛一定要 正视弹簧测力计的刻度 ,要按有效数字正确读数和记录. ② 减小作图误差的方法:21F F 与夹角适宜,且比例要恰当。 六、注意事项: ①位置不变:在同一次实验中,使橡皮条拉长时 结点 的位置一定要相同. ②角度合适:用两个弹簧测力计钩住细绳套互成角度地拉橡皮条时,其夹角不宜太 小 ,也不宜太大,以60°~120°之间为宜. ③ 尽量减少误差:在合力不超出量程及在橡皮条弹性限度内形变应尽量大一些;细绳套应适当长一些,便于确定力的方向. ④ 统一标度:在同一次实验中,画力的图示选定的标度要相同,并且要恰当选定标度,使力的图示稍大一些. 〖考点1〗对实验原理及实验过程的考查 【例1】在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上, 先用一个弹簧秤拉橡皮条的另一端到某一点并记下该点的位置;再将橡皮条的另一端系两根细绳,细绳的另一端都有绳套,用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条. ⑴ 某同学认为在此过程中必须注意以下几项: A .两根细绳必须等长 B .橡皮条应与两绳夹角的平分线在同一直线上 C .在使用弹簧秤时要注意使弹簧秤与木板平面平行 D .在用两个弹簧秤同时拉细绳时要注意使两个弹簧秤的读数相等 E .在用两个弹簧秤同时拉细绳时必须将橡皮条的另一端拉到用一个弹簧秤拉时记下的位置 其中正确的是_______________(填入相应的字母) ⑵ “验证力的平行四边形定则”的实验情况如图甲所示,其中A 为固定橡皮条的图钉,O 为橡皮条与细绳的结点,OB 和OC 为 细绳.图乙是在白纸上根据实验结果画出的力的示意图. ① 图乙中的F 与F′两力中,方向一定沿AO 方向的是______; ② 本实验采用的科学方法是________ A .理想实验法 B .等效替代法 C .控制变量法 D .建立物理模型法 ⑶ 某同学在坐标纸上画出了如图所示的两个已知力F 1和F 2,图中小正方形的边长表示2 N ,两力的合力用F 表示,F 1、F 2与F 的夹角分别为θ1和θ2,关于F 1、F 2与F 、θ1和θ2关系正确的有________ A .F 1 = 4N B .F = 12 N C .θ1 = 45° D .θ1 < θ2
中考数学解题策略专题02 平行四边形的存在性问题
中考数学解题策略专题02 平行四边形的存在性问题 专题攻略 解平行四边形的存在性问题一般分三步: 第一步寻找分类标准,第二步画图,第三步计算. 难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快. 如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况. 根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便. 例题解析 例?如图1-1,在平面直角坐标系中,已知抛物线 y=-x2-2x+3与x轴交于A、B两点(A在B的左侧), 与y轴交于点C,顶点为P,如果以点P、A、C、D为 顶点的四边形是平行四边形,求点D的坐标. 图1-1 例?如图2-1,在平面直角坐标系中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标. 图2-1
例? 如图3-1,在平面直角坐标系中,直线y =-x +4与x 轴交于点A ,与y 轴交于点B ,点C 在直线AB 上,在平面直角坐标系中求一点D ,使得以O 、A 、C 、D 为顶点的四边形是菱形. 图 3-1 例? 如图4-1,已知抛物线241633 y x x =+与x 轴的负半轴交于点C ,点E 的坐标为(0,-3),点N 在抛物线的对称轴上,点 M 在抛物线上,是否存在这样的点M 、N ,使得以M 、N 、C 、E 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若 不存在,请说明理由. 图4-1 例?如图1,在平面直角坐标系中,抛物线y =ax 2-2ax -3a (a <0)与x 轴交于A 、B
二次函数中特殊四边形的存在性问题
网课:二次函数中特殊四边形的存在性问题 学习目标: 1、通过二次函数中的特殊四边形存在性问题的探究、学习,获取解决这类问题的基本方法;经历解决二次函数中的特殊四边形存在性问题的探索过程,培养学生的理解能力,抽象能力,能正确认识问题的本质,提高知识迁移能力,积累解决问题的经验,感受数学知识对解决问题的价值; 2、通过函数中的特殊四边形存在性问题的解决,渗透“转化”、“分类”、“方程”、“数形结合”等数学思想,并在问题解决中体验成功的快乐,感受数学的魅力. 学习重点:利用“特殊四边形的性质”,或者“点在函数上”来建立等量关系,解决“点是否存在的问题”. 学习难点:从复杂的函数背景中提炼问题的本质,利用“特殊四边形的性质”,或者“点在函数上”来建立等量关系,解决“点是否存在的问题”. 背景问题: 如图,抛物线中,点A在x轴的正半轴上,点C在y轴的正半轴上, OC=3,点D是直线AC与抛物线的交点。 问题一:在平面内是否存在一点B,使得以A、B、O、D为顶点的 四边形是平行四边形? 若存在,请直接写出B点的坐标;若不存在,请说明理由。 归纳:_________________________________________________ 问题二:若点M在抛物线上,点N在x轴上,是否存在以A、D、M、N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由; (备图1)(备图2) 归纳: _____________________________________________________________________________
问题三:若点E(2,3)在抛物线上,点F、P在直线AC上,当EF所在直线与x轴垂直时,平面内是否存在一点Q,使得以点E、F、P、Q为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由; (备图1)(备图2) 归纳: ______________________________________________________________________________ 问题四:点是直线AC上一点,若点N是平面内一点,M是抛物线对称轴上的一点,是否存在一点M使得以点A,P,M,N为顶点的四边形是矩形?若能,求出点M的坐标;若不能,请说明理由. 归纳: _______________________________________________________________________
实验 探究力的平行四边形定则
实验验证力的平行四边形定则 一、【实验目的】 1.会使用弹簧测力计. 2.验证互成角度的两个力合成时的平行四边形定则. 二、【实验原理】 1.等效法:使一个力F′的作用效果和两个力F1、F2的作用效果都是让同一条一端固定的橡皮条伸长到同一点,所以一个力F′就是这两个力F1和F2的合力,作出力F′的图示,如图所示. 2.平行四边形法:根据平行四边形定则作出力F1和F2的合力F的图示. 3.验证:比较F和F′的大小和方向是否相同,若在误差允许的范围内相同,则验证了力的平行四边形定则. 三、【实验器材】
方木板、白纸、弹簧测力计、橡皮条、细绳套、三角板、刻度尺、图钉、铅笔 四、【实验步骤】 (1)安装好实验器材,用两个弹簧测力计分别勾住绳套,互成角度拉橡皮条,使橡皮条伸长,结点达到某一位置O,如图所示,记下两弹簧的读数F1 F2,及两条细绳的方向。 (2)只用一只弹簧测力计,通过细绳把橡皮条的结点拉到同样的位置O,读出并记录弹簧测力计的读数F′,同时记下细绳的方向.(3)按照相同的标度作出F1,F2及F~的图示,比较F与F′的差异。(4)做完实验,整理仪器,有序退场。 .
五、【实验数据处理】 ①作力的合成图,要使用刻度尺和圆规作图,将图画的适当的大 一些、美观、准确,要严格按力的图示要求和几何作图法作出合力。 ②由作平行四边形法得到的F和实际测量得到的F~不可能完全重 合,一般大小和方向的偏差在10%以内(角度在5度以内),即可认为验证了平行四边形定则。 六、【实验注意事项】 1、使用弹簧测力计前,要先观察指针是否指在零刻度处,否则要调零;再将两个弹簧测力计的挂钩钩在一起,向相反方向拉,如果两个示数相同可使用(另外本实验不需要量角器,按照拉力角度作图即可) 2、试验中的两个细绳套不要太短,适当长度即可;两个拉力的夹角不宜太大或太小,在60-100之间为宜,拉力角度不需要垂直。 3、在同一实验中,使橡皮条拉长时结点的位置一定要相同,每次一定要同时记下拉力的大小和对应的方向。 4、拉力应沿弹簧测力计的轴线方向;弹簧测力计中弹簧轴线、橡皮条、细绳套应该位于与纸面平行的同一平面。 5、在同一实验中,画力的图示选定的标度要相同,并且要恰当。 特别提醒:记录每一次结点O的位置(保证作用效果一样) 每次拉力的大小以及它的方向 F是理论值(平行四边形的对角线) F′是实验值,与OA共线。
二次函数平行四边形存在性问题例题
二次函数平行四边形存在性问题例题 一.解答题(共9小题) 1.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点. (1)求抛物线的解析式; (2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标; (3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. 2.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧). (1)求抛物线的解析式及点B坐标; (2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值; (3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由. 3.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点
分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x 轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若(1)中抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)若把(1)中的抛物线向左平移3.5个单位,则图象与x轴交于F、N(点F 在点N的左侧)两点,交y轴于E点,则在此抛物线的对称轴上是否存在一点Q,使点Q到E、N两点的距离之差最大?若存在,请求出点Q的坐标;若不存在,请说明理由. 4.已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C. (1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式; (2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由; (3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA ﹣QO|的取值范围. 5.如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,
(完整版)一次函数与特殊四边形存在性问题(培优拓展)
一次函数与特殊四边形的存在性问题 (培优专题) 1.(2015春?通州区校级期中)如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由. 2.(2015春?北京校级期中)已知直线y=x+3分别交x轴、y轴于点A、B. (1)求∠BAO的平分线的函数关系式;(写出自变量x的取值范围) (2)点M在已知直线上,点N在坐标平面内,是否存在以点M、N、A、O 为顶点的四边形为菱形?若存在,请直接写出点N的坐标;若不存在,说明理由.
3.(2010秋?吴江市校级期中)已知:如图,在矩形ABCD中,点E在AD 边上,AE>DE,BE=BC,点O是线段CE的中点. (1)试说明CE平分∠BED; (2)在直线AD上是否存在点F,使得以B、C、F、E为顶点的四边形是菱形?如果存在,试画出点F的位置,并作适当说明;如果不存在,请说明理由. 4.如图,在平面直角坐标系xOy,直线y=x+1与y=﹣2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
5.如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l 的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由. 6.(2012春?雨花区校级期末)如图,已知等边△ABC的边长为2,顶点A、B分别在x轴、y轴的正半轴上移动. (1)当OA=时,求点C的坐标. (2)在(1)的条件下,求四边形AOBC的面积. (3)是否存在一点C,使线段OC的长有最大值?若存在,请求出此时点C 的坐标;若不存在,请说明理由.
一次函数与四边形存在性问题
一次函数与四边形综合专题 1.如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与对角线AC交于Q点 (Ⅰ)若点P的坐标为(1,),求点M的坐标; (Ⅱ)若点P的坐标为(1,t) ①求点M的坐标(用含t的式子表示)(直接写出答案) ②求点Q的坐标(用含t的式子表示)(直接写出答案) (Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由. 2.如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F. (1)求直线AB的解析式; (2)若四边形POEF是平行四边形,求点P的坐标; (3)是否存在点P,使△PEF为直角三角形?若存在,请直接写出点P的坐标;
若不存在,请说明理由. 3.如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B 的坐标分别A (,0)、B(,2),∠CAO=30°. (1)求对角线AC所在的直线的函数表达式; (2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标; (3)在平面是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由. 4.如图,直线l与坐标轴分别交于A、B两点,∠BAO=45°,点A坐标为(8,0).动点P从点O出发,沿折线段OBA运动,到点A停止;同时动点Q也从点O出发,沿线段OA运动,到点A停止;它们的运动速度均为每秒1个单位长度. (1)求直线AB的函数关系式; (2)若点A、B、O与平面点E组成的图形是平行四边形,请直接写出点E的坐标; (3)在运动过程中,当P、Q的距离为2时,求点P的坐标. 5.在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒. (1)当点P移动到点D时,t=秒;
实验验证平行四边形定则和胡克定律
.. 讲义编号: 2.5实验验证平行四边形法则 探究弹力与弹簧伸长的关系 知识梳理 一、验证力的平行四边形定则 1.实验目的 验证互成角度的两个力合成时的平行四边形定则. 2.实验原理 ①等效法:使一个力F′的作用效果和两个力F1、F2的作用都是让同一条一端固定的橡皮条伸长到某点,所以一个力F′就是这两个力F1和F2的合力,作出力F′的图示,如图所示. ②平行四边形法:根据平行四边形定则作出力F1和F2的合力F的图示. ③验证:比较F和F′的大小和向是否相同,若有误差允的围相同,则验证了力的平行四边形定则. 3.实验器材 木板、白纸,弹簧测力计(两只),橡皮条,细绳套(两个),三角板,刻度尺,图钉(几个).4.实验步骤 ①用图钉把白纸钉在水平桌面上的木板上. ②用图钉把橡皮条的一端固定在A点,橡皮条的另一端拴上两个细绳套. Word资料.
③用两只弹簧测力计分别钩住细绳套,互成角度地拉橡皮条,使橡皮条与绳的结点伸长到某一位置O,如图所示,记录两弹簧测力计的读数,用铅笔描下O 点的位置及此时两细绳的向. ④用铅笔和刻度尺从结点O沿两条细绳向画直线,按选定的标度作出这两只弹簧测力计的拉力F1和F2的图示,并以F1和F2为邻边用刻度尺作平行四边形,过O点画平行四边形的对角线,此对角线即为合力F的图示. ⑤只用一只弹簧测力计通过细绳套把橡皮条的结点拉到同样的位置O,记下弹簧测力计的读数和细绳的向,用刻度尺从O点按同样的标度沿记录的向作出这只弹簧测力计的拉力F′的图示. ⑥比较力F′与平行四边形定则求出的合力F在大小和向上是否相同. ⑦改变两个力F1和F2的大小和夹角,再重复实验两次. 5.实验注意事项 ①在同一次实验中,使橡皮条拉长时结点的位置一定要相同. ②用两个弹簧测力计钩住细绳套互成角度地拉橡皮条时,其夹角不宜太小,也不宜太大,以60°~100°之间为宜. ③读数时应注意使弹簧测力计与木板平行,并使细绳与弹簧测力计的轴线在同一条直线上,避免弹簧与测力计外套、弹簧测力计的限位卡之间有摩擦.读数时眼睛要正视弹簧测力计刻度,在合力不超出量程及橡皮条在弹性限度的前提下,测量数据尽量大一些. ④细绳应适当长一些,便于确定力的向.不要直接沿细绳向画直线,应在细绳两端画两个射影点.取掉细绳后,连直线确定力的向. ⑤以调零后的弹簧测力计的两挂钩互钩后对拉,读数相同为宜. ⑥在同一次实验中,画力的图示选定的标度要相同,并且要恰当选定标度,使力的图示稍大一些. 6.实验误差分析 ①读数误差 减小读数误差的法:弹簧测力计数据在允的情况下,尽量大一些.读数时眼睛一定要正视刻度尺,要按有效数字正确读数和记录. ②作图误差 减少作图误差的法:作图时两力的对边一定要平行.两个分力F1、F2间的夹角越大,用平行四边形作出的合力F的误差ΔF就越大,所以实验中不要把F1、F2间的夹角取得太大.二、探究弹力和弹簧伸长的关系 1.实验目的 ①探究弹力和弹簧伸长的关系. ②学会用列表法和图象法处理实验数据. ③培养用所学知识探究物理规律的能力. 2.实验原理 在竖直悬挂的轻弹簧下端悬挂钩码,平衡时弹力大小等于钩码的重力.用刻度尺量出弹簧的
中考数学压轴题:特殊四边形存在性问题
?? ?? 探究特殊四边形存在性问题 1.如图,抛物线y=x2-2x-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB. (1)求点B,C的坐标; (2)若点D在y轴上,且∠BDO=∠BAC,求点D的坐标; (3)若点M为抛物线上一点,点N在抛物线的对称轴上,是否存在以点A、B、M、N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标,若不存在,请说明理由. 第1题图 解:(1)令x=0得y=-3, ∴C(0,-3), ∴OC=3, ∵OC=3OB, ∴OB=1, ∴B(-1,0), 把A(2,-3),B(-1,0)分别代入y=ax2+bx-3得: ?a-b-3=0?a=1 ?,解得?, ?4a+2b-3=-3?b=-2 ∴抛物线的解析式为y=x2-2x-3; (2)如解图①,过点B作BE⊥AC,交AC延长线于点E. 第1题解图① ∵C(0,-3),A(2,-3), ∴AC∥x轴, ∴BE=3, 又∵OB=1, ∴AE=3,∴AE=BE,
∴∠BAE=45°, ∵∠BDO=∠BAC=45°, ∴OB=OD, ∴D点的坐标为(0,1)或(0,-1), (3)存在.如解图②. 第2题解图② 当AB∥MN时,由AB=MN=32,可知点M与对称轴的距离为3,由y=x2-2x-3可得对称轴为直线x=1, ∴点M的横坐标为4或-2,把x=4和-2分别代入y=x2-2x-3可得点M坐标, 把x=-2代入y=x2-2x-3得y=4+4-3=5, (-2,5). ∴M 1 把x=4代入y=x2-2x-3得y=16-8-3=5, (4,5), ∴M 2 当MN与AB互相平分时,四边形AMBN是平行四边形,由AC=BN=2,可知点M与点C重合,∴点M3坐标为(0,-3), ∴M的坐标为(-2,5)或(0,-3)或(4,5). 2.如图,抛物线顶点P(1,4),与y轴交于点C(0,3),与x轴交于点A,B. (1)求抛物线的解析式; (2)Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标; (3)若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E,是否存在点M,N使四边形MNED为正方形?如果存在,求正方形MNED的边长;如果不存在,请说明理由. 第2题图 解:(1)设抛物线解析式为:y=a(x-1)2+4(a≠0). ∵抛物线过点C(0,3), ∴a+4=3,∴a=-1. ∴y=-(x-1)2+4=-x2+2x+3; (2)由(1)得,抛物线的解析式为y=-x2+2x+3,
平行四边形之存在性问题
中考数学压轴题解题策略 综合题之平行四边形存在性问题 专题攻略 解平行四边形的存在性问题一般分三步: 第一步寻找分类标准,第二步画图,第三步计算. 难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快. 如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况. 根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便. 例题解析 例1、如图1-1,在平面直角坐标系中,已知抛物 线y=-x2-2x+3与x轴交于A、B两点(A在B的左 侧),与y轴交于点C,顶点为P,如果以点P、A、C、D 为顶点的四边形是平行四边形,求点D的坐标. 图1-1 【解析】P、A、C三点是确定的,过△PAC的三个顶点分别画对边的平行线,三条直线两两相交,产生3个符合条件的点D(如图1-2). 由y=-x2-2x+3=-(x+1)2+4,得A(-3,0),C(0, 3),P(-1, 4). 由于A(-3,0)33 右,上D1(2, 7). 右,上C(0, 3),所以P(-1, 4)33 由于C(0, 3)33 下,左A(-3,0),所以P(-1, 4)33 下,左D2(-4, 1).由于P(-1, 4)11 右,下D 3(-2, -1). 右,下C(0, 3),所以A(-3,0)11 我们看到,用坐标平移的方法,远比用解析式构造方程组求交点方便多了. 图1-2
常见四边形的存在性
常见四边形的存在性 专题一、平行四边形的存在性问题 一、技巧提炼 模型:平行四边形模型探究 如图1,点A ()11,x y 、B ()22,x y 、C ()33,x y 是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D ,使得以A 、B 、C 、D 四点为顶点的四边形为平行四边形,如果存在,请求出点D 的坐标。 A B C x y 图1 图2 如图2,过A 、B 、C 分别作BC 、AC 、AB 的平行线,则以不在同一直线上的三点为顶点的平行四边形有三个。由已知的三点坐标可根据图形平移的坐标性质,直接写出第四个顶点的坐标。 解题思路:(1)先分类(2)再画图(3)后计算 例1.(2015?贵阳)如图,经过点C (0,﹣4)的抛物线y=ax 2 +bx+c (a≠0)与x 轴相交于A (﹣2,0),B 两点. (1)a > 0,b 2 ﹣4ac > 0(填“>”或“<”); (2)若该抛物线关于直线x=2对称,求抛物线的函数表达式; (3)在(2)的条件下,连接AC ,E 是抛物线上一动点,过点E 作AC 的平行线交x 轴于点F .是否存在这样的点E ,使得以A ,C ,E ,F 为顶点所组成的四边形是平行四边形若存在,求出满足条件的点E 的坐标;若不存在,请说明理由.
【考点】二次函数综合题. 【专题】综合题;压轴题. 【分析】(1)根据抛物线开口向上,且与x轴有两个交点,即可做出判断; (2)由抛物线的对称轴及A的坐标,确定出B的坐标,将A,B,C三点坐标代入求出a,b,c的值,即可确定出抛物线解析式; (3)存在,理由为:假设存在点E使得以A,C,E,F为顶点所组成的四边形是平行四边形,过点C作CE∥x轴,交抛物线于点E,过点E作EF∥AC,交x轴于点F,如图1所示;假设在抛物线上还存在点E′,使得以A,C,F′,E′为顶点所组成的四边形是平行四边形,过点E′作E′F′∥AC交x轴于点F′,则四边形ACF′E′即为满足条件的平行四边形,可得AC=E′F′,AC∥E′F′,如图2,过点E′作E′G⊥x轴于点G,分别求出E坐标即可.【解答】解:(1)a>0,b2﹣4ac>0; (2)∵直线x=2是对称轴,A(﹣2,0), ∴B(6,0), ∵点C(0,﹣4),将A,B,C的坐标分别代入y=ax2+bx+c,
平行四边形定则应用
平行四边形定则应用 1.如图1-5-12所示,用轻绳AO和OB将重为G的重物悬挂在水平天花板和竖直墙壁之间处于静 止状态,AO绳水平,OB绳与竖直方向的夹角为θ.则AO绳的拉力T1、OB绳的拉力T2的大小与 G之间的关系为()A.T1=G tanθ B.T1= C.T2= D.T2=G cosθ 2.如 图所示,一个半径为r、重为G的圆球,被长为r的细绳挂在竖直的光滑的墙壁上,绳与墙所成的角度为30°,则绳子的拉力T和墙壁的弹力N分别是( ) A.T=G, B.T=2G,N=G C. D. 3.如图所示,在倾角为45°的光滑斜面上有一圆球,在球前放一光滑挡板使球保持静止, 此时球对斜面的正压力为N1;若去掉挡板,球对斜面的正压力为N2,则下列判断正确的是 A.B.N2=N1C.N2=2N1D. 4.如图是某同学为颈椎病人设计的一个牵引装置的示意图,一根绳绕过两个定滑轮和 动滑轮后各挂着一个相同的重物,与动滑轮相连的帆布带拉着病人的颈椎(图中是用手指 代替颈椎做实验),整个装置在同一竖直平面内。如果要增大手指所受的拉力,可采取的方法是A.只增加绳的长度 B.只增加重物的重量 C.只将手指向下移动 D.只将手指向上移动 5.如图所示,在倾角为α的斜面上,放一质量为m的小球,小球和斜坡及挡板间均无摩擦,当 档板绕O点逆时针缓慢地转向水平位置的过程中,则有() A.斜面对球的支持力逐渐增大 B.斜面对球的支持力逐渐减小 C.档板对小球的弹力先减小后增大 D.档板对小球的弹力先增大后 减小 6.用一轻绳将小球P系于光滑墙壁上的O点,在墙壁和球P之间夹有 一矩形物块Q,如图所示。P、Q均处于静止状态,则下列相关说法正确 的是() A.P物体受4个力 B.Q受到3个力 C.若绳子变长,绳子的拉力将变小 D.若绳子变短,Q受到的静摩擦力将增大 8.一光滑大圆球固定在地上,O点为其球心,一根轻细绳跨在圆球上,绳的两端分别系有 质量为m1和m2的小球(小球半径忽略不计),当它们处于平衡状态时,质量为m1的小球与 O点的连线与竖直方向的夹角θ =60°,两小球的质量比m1:m2为() A. B. C. D. 9.如图所示,将一球形物体夹在竖直墙AC与木板BC之间,已知各接触面均光滑,将球对墙的压力 用N1表示,球对木板的压力用N2表示.现将木板以C端为轴缓慢地转至水平位置的过程中,下列说 法中正确的是() A、N1和N2都增大 B、N1和N2都减小 C、N1增大, N2减小 D.、N1减小, N2增大 10.如图所示,放在光滑斜面上的小球,一端系于固定的O点,现用外力缓慢将斜面在水平桌面 上向左推移,使小球上升(最高点足够高),在斜面运动过程中,球对绳的拉力将() A.先增大后减小B.先减小后增大 C.一直增大D.一直减小
四边形之存在性问题(讲义及答案)
四边形之存在性问题(讲义) 课前预习 一般悄况下我们如何处理存在性问题? (1) 研究背景图形 坐标系背景下研究 ____________ 、 ______ 究 ___________ 、 ____________ 、 ______ (2) 根据不变特征,确定分类标准 研究定点,动点,定线段,确定分类标准 不变特征举例: ① 等腰三角形(两定一动) 以定线段作为 ________ 或者— _______________ 确定点的位 ② 置.等腰直角三角形(两定 一动) 以 知识点睛 存在性问题处理框架: ① 研究背景图形. ② 根据不变特征,确定分类标准. ③ 分析特殊状态的形成因素,画出符合题意的图形并求解. ④ 结果验证. 平行四边形存在性问题特征举例: 分析定点、动点. ① 三定一动,连接定点出现三条定线段.定线段分别作 为平行四边形的 _________ ,利用 _____________ 确定 点坐标. ② 两定两动,连接定线段,若定线段作为平行四边形的 ________ ,则通过 ___________ 确定点的坐标;若定线 段作为平行四边形的 ___________ ,则定线段绕 __________ 旋转,利用 _______________ 确定点的坐标. 结合图形进行验证. ;儿何图形研 或者 来分类,利用 来分类,然后借助 确定点的位置. (3) 分析特殊状态的形成因素,画出符合题意的图形并求解 (4) 结果验证 2. (1) (2)
3.特殊平行四边形存在性问题不变特征举例: ①菱形存在性问题(两定两动) 转化为等腰三角形存在性问题; 以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,然后通过平移确定另一动点坐标. ②正方形存在性问题(两定两动) 转化为等腰直角三角形存在性问题; 根据直角顶点确定分类标准,利用两腰相等或者45。角确定一动点的位置,然后通过平移确定另一动点坐标. 2如图,在平面直角坐标系中,直线y = -?x + 3与X轴、>' 4 轴分别交于点A, 点C的坐标为(0, -2 ).若点D在直线 AB上运动,点E在直线AC±运动,当以0, 4, D, E为顶点的四边形是平行四边形时,求点D的坐标.
向量的平行四边形法则运用
向量基本定理与平行四边形法则运用 1. 已知点P 是△ABC 所在平面上一点,且 1 3 AP AB t AC = + ,t 为实数,若点P 在△ABC 内部(不包括边界),则t 的取值范围为20,3? ? ?? ? 2. 在 四 边 形 ABCD 中, () 1,1AB DC ==, 113 BA BC BD BA BC BD + = ,则四边形ABCD 3. 已知平面向量a ,b 满足||1a =,||2b =,且()a b a +⊥,则a 与的 夹角是 A . 56π B .23π C .3π D . π 6 4. 在ABC ?中,M 是BC 的中点,3AM =,点P 在AM 上,且满足 2AP PM =,则()PA PB PC ?+的值为 A. 4- B.2- C.2 D. 4 5. 半圆的直径AB=6,O 为圆心,C 为半圆上不同于A ,B 的任意一点, 若P 为半径OC 上动点,则()PC PB PA ?+的最小值为9 2 -. 6. 若等边ABC ?的边长为平面内一点M 满足12 63 CM CB CA =+, 则MA MB ?=-2 7. 若非零向量、满足 2a b a b a -=-=,a 与a b +的夹 角为 060 8. 已知()0,3-A ,() 3,0B ,O 为坐标原点,点C 在AOB ∠内,且 60AOC ∠=,设+=λ,则实数λ等于 3 1
9. 梯形ABCD 中,DA=AB=BC=1,CD=2,点P 在△BCD 内部(包括 边界)中运动,则AP BD ?的取 值范围是3 3, 2 2??-???? 坐标处理比较方便. 10. 平面上三点O 、A 、B 不共线,求证:平面上任一点C 与A 、B 共线 的充要条件是存在实数λ和μ,使OC =λOA + μOB ,且λ+ μ = 1。 证:必要性:设A ,B ,C 三点共线,则可设= t (t ∈R) 则=+=+ t =+ t (-) = (1-t )+ t 令1-t =λ,t = μ,则有:=λ+ μ,且λ+ μ = 1 充分性:AC =OC -OA =λOA + μOB -OA = (λ-1)OA + μOB = -μOA + μOB = μ(OB -OA ) = μAB ∴三点A 、B 、C 共线 练习: 11. (2007江西)如图,在△ABC 中,点O 是BC 的中点,过点O 的直 线分别交直线AB ,AC 于点M ,N ,若AB m AM =,AC n AN =,则m n +=
平行四边形的存在性问题
平行四边形的存在性问题 专题攻略 解平行四边形的存在性问题一般分三步: 第一步寻找分类标准,第二步画图,第三步计算. 难点在于寻找分类标准,分类标准寻找的恰当,可以使得解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点. 如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况. 灵活运用向量和中心对称的性质,可以使得解题简便. 针对训练 1.如图,已知抛物线y=-x2-2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为P.若以A、C、P、M为顶点的四边形是平行四边形,求点M的坐标. 解析、由y=-x2-2x+3=-(x+3)(x-1)=-(x+1)2+4, 得A(-3,0),B(1,0),C(0,3),P(-1,4). 如图,过△P AC的三个顶点,分别作对边的平行线,三条直线两两相交的三个交点就是要求的点M. ①因为AM1//PC,AM1=PC,那么沿PC方向平移点A可以得到点M1. 因为点P(-1,4)先向下平移1个单位,再向右平移1个单位可以与点C(0,3)重合,所以点A(-3,0)先向下平移1个单位,再向右平移1个单位就得到点M1(-2,-1). ②因为AM2//CP,AM2=CP,那么沿CP方向平移点A可以得到点M2. 因为点C(0,3)先向左平移1个单位,再向上平移1个单位可以与点P(-1,4)重合,所以点A(-3,0)先向左平移1个单位,再向上平移1个单位就得到点M2(-4,1). ③因为PM3//AC,PM3=AC,那么沿AC方向平移点P可以得到点M3. 因为点A(-3,0)先向右平移3个单位,再向上平移3个单位可以与点C(0,3)重合,所以点P(-1,4)先向右平移3个单位,再向上平移3个单位就得到点M3(2,7). 2.如图,在平面直角坐标系xOy中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标. 解析.由y=-x2+2x+3=-(x+1)(x-3),得A(-1,0),B(3,0). ①如图1,当AB是平行四边形的对角线时,PM与AB互相平分,因此点M与点P关于AB 的中点(1,0)对称,所以点M的横坐标为2. 当x=2时,y =-x2+2x+3=3.此时点M的坐标为(2,3).
四边形之存在性问题(二)(讲义及答案)
四边形之存在性问题(二)(讲义) 课前预习 1.一般情况下我们如何处理存在性问题? (1)研究背景图形 坐标系背景下研究、;几何图形研究、、. (2)根据不变特征,确定分类标准 研究定点,动点,定线段,确定分类标准 不变特征举例: ①等腰三角形(两定一动) 以定线段作为或者来分类,利用 确定点的位置. ②等腰直角三角形(两定一动) 以来分类,然后借助或者 确定点的位置. (3)分析特殊状态的形成因素,画出符合题意的图形并求解(4)结果验证 2.用铅笔做讲义第1,2 题,并将计算、演草保留在讲义上,先 看知识点睛,再做题,思路受阻时(某个点做了2~3 分钟)重复上述动作,若仍无法解决,课堂重点听. 知识点睛 1.存在性问题处理框架: ①研究背景图形. ②根据不变特征,确定分类标准. ③分析特殊状态的形成因素,画出符合题意的图形并求解. ④结果验证. 2.特殊平行四边形存在性问题不变特征举例: ①菱形存在性问题(两定两动) 转化为等腰三角形存在性问题; 以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,然后通过平移确定另一动点坐标. ②正方形存在性问题(两定两动)转 化为等腰直角三角形存在性问题; 根据直角顶点确定分类标准,利用两腰相等或者45°角确定一动点的位置,然后通过平移确定另一动点坐标.
精讲精练 1.如图,在平面直角坐标系xOy 中,直线l:y = 2x - 4 与x 轴交 于点A,与y 轴交于点B. (1)求点A,B 的坐标. (2)若P 是直线x =-2 上的一动点,则在坐标平面内是否存在点Q,使得以A,B,P,Q 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.
平行四边形存在性问题
平行四边形存在性问题 一、解平行四边形的存在性问题一般分三个步骤 第一步寻找分类标准,第二步画图,第三步计算. 二、难点在于寻找分类标准,寻找恰当的分类标准,可以使得解的个数不重复不遗漏,也可以使计算又准又快. 三、如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点,利用横纵坐标的平移变化得出结论。 四、如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况,灵活运用向量和中心对称的性质,可以使得解题简便。(辅助手段~三角形全等,等积法,中点坐标公式) 例1.已知抛物线 b ax ax y ++-=22 与x 轴的一个交点为A(-1,0),与y 轴的正半轴交于点C . ⑴直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点B 的坐标; ⑵当点C 在以AB 为直径的⊙P 上时,求抛物线的解析式; ⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由. 例2、如图,抛物线:y= x 2﹣x ﹣ 与x 轴交于A 、B (A 在B 左侧),A (﹣1,0)、B (3,0),顶点为C (1,﹣2)(1)求过A 、B 、C 三点的圆的半径.(2)在抛物线上找点P ,在y 轴上找点E ,使以A 、B 、P 、E 为顶点的四边形是平行四边形,求点P 、E 的坐标. 例 3.已知,如图抛物线
23(0)y ax ax c a =++>与y 轴交于C 点,与x 轴交于A 、B 两点,A 点在B 点左侧。点B 的坐标为(1,0),OC=30B .(1)求抛物线的解析式;(2)若点D 是线段AC 下方抛物线上的动点,求四边形ABCD 面积的最大值: (3)若点E 在x 轴上,点P 在抛物线上。是否存在以A 、C 、E 、P 为顶点且以AC 为一边的平行四边形?若存在,求点P 的坐标;若不存在,请说明理由. 例4.已知抛物线:x x y 22 12 1+- = (1)求抛物线1y 的顶点坐标. (2)将抛物线1y 向右平移2个单位,再向上平移1个单位,得到抛物线2y ,求抛物线2y 的解析式. (3)如下图,抛物线2y 的顶点为P ,x 轴上有一动点M ,在1y 、2y 这两条抛物线上是否存在点N ,使O (原点)、P 、M 、 N 四点构成以OP 为一边的平行四边形, 若存在,求出N 点的坐标;若不存在,请说明理由. 例5.如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2. (1)求A 、B 两点的坐标及直线AC 的函数表达式; (2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值; (3)点G 抛物线上的动点,在x 轴上是否存在点F ,使A 、C 、F 、G 这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F 点坐标;如果不存在,请说明理 x y y 12 3 4 5 6 7 8 9 54321 -1-2-3-4 1 y 2 -1
