高级计量经济学之第5章分布滞后与动态模型

第5章 分布滞后与动态模型
§5.1 分布滞后模型
很多经济模型在回归方程中有滞后项,例如,因为修建桥和高速公路需要很多时间,所以公共投资对GDP 的影响有一个滞后期,而且这个影响可能会持续数年;研发新产品需要时间,而后把这个新产品投入生产也需要时间;在研究消费行为时,一个工资的变化可能影响好几期的消费。在消费的恒久收入理论中,消费者会用若干期去决定真实可支配收入的变化是暂时的还是永久的。例如,今年额外的咨询费收入明年是否还会继续?同样,真实可支配收入的滞后值会在回归方程中出现,是因为消费者在平滑其消费行为时十分重视他自身的终身收入。一个人的终身收入可以用他过去和现在的收入来推测。换句话说,回归关系可以写为:
T t X X X Y t
s t s t t t ,,2,1110 =+++++=--εβββα (5.1)
其中,t Y 代表被解释变量Y 在第t 期的观测值,t s X -代表解释变量X 第t s -期的观测值,α为截距项,0β,1β,…,s β是t X 当期和滞后期的系数。方程(5.1)式就是分布滞后模型因为它把收入增长对消费的影响分为s 期。X 的一个单位变化对Y 的短期影响由0β来表示,而X 的一个单位变化对Y 的长期影响由
(s βββ+++ 10)来表示。
假设我们观察从1955年到1995年的t X ,1t X -为相同的变量,但是提前一期的,也就是1954-1994。因为1954年的数据观察不到,我们就从1955年开始观察
1t X -,到1994年结束。这意味着当我们滞后一期时,t X 序列将从1956年开始到
1995年结束。对于实际的应用来说,也就是当我们滞后一期时,我们将从样本中
丢失了一个观测值。所以如果我们滞后s 期,将丢失s 个观测值。更进一步,对于每一个滞后值,都要估计出一个额外的β值。因此,自由度会产生双重损失,即观测值数目的减少(因为引进滞后项),以及所需估计的参数增加。除了自由度的丢失以外,方程(5.1)式的解释变量相互间还可能存在高度相关。事实上,大部分经济时间序列通常存在趋势,和它们的滞后值间存在高度相关。这些解释变量的多重共线性程度越高,回归估计的可行性就越低。
对于这个模型,OLS 仍旧是BLUE ,因为仍然满足经典线性回归的基本假设。在方程(5.1)式中我们所做的就是引入额外的自变量(s t t X X --,,1 )。这些变量与随机误差项不相关,因为它们都滞后于变量t X ,而t X 假设与t ε无关。
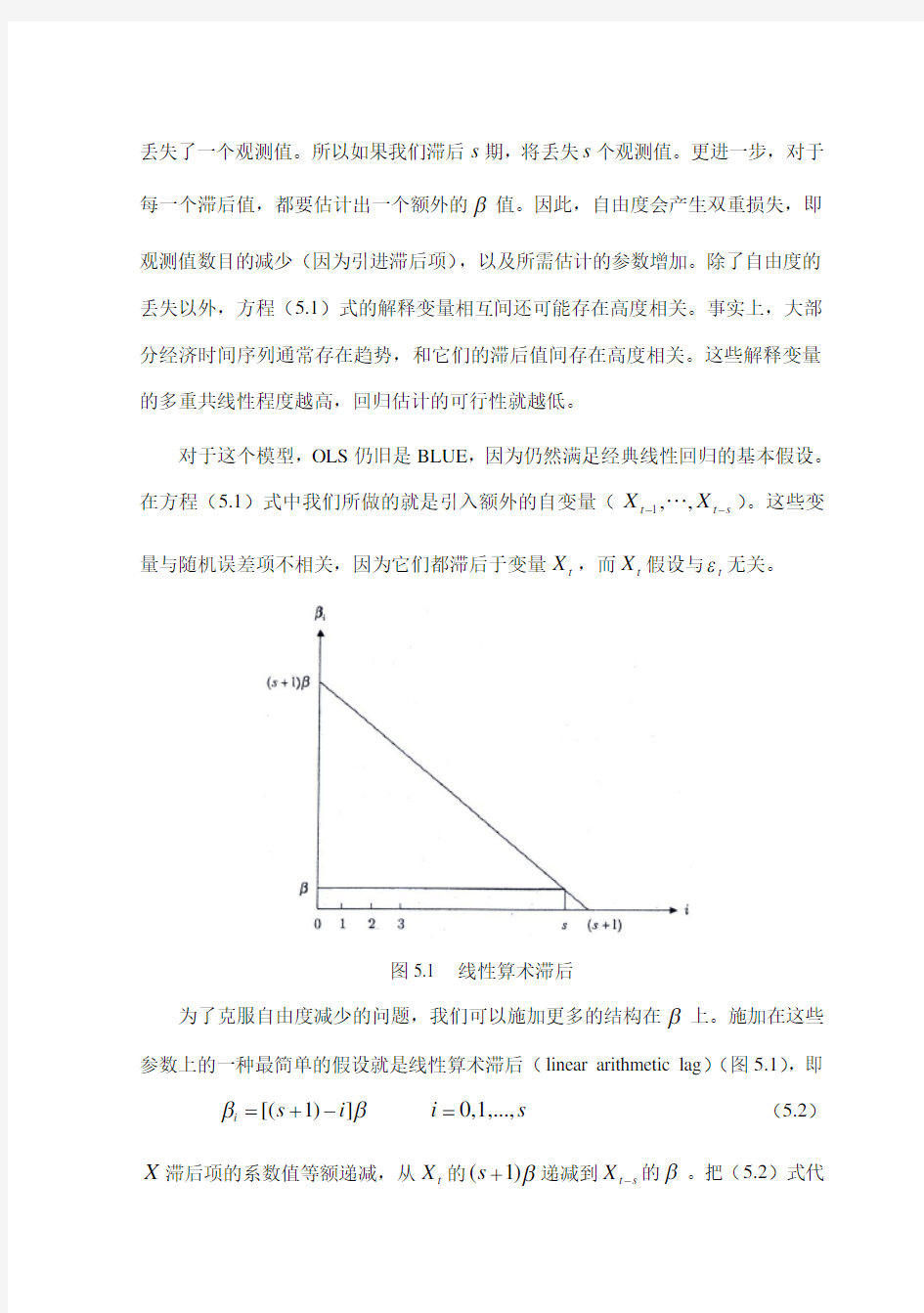
图5.1 线性算术滞后
为了克服自由度减少的问题,我们可以施加更多的结构在β上。施加在这些参数上的一种最简单的假设就是线性算术滞后(linear arithmetic lag )(图5.1),即
[(1)]i s i ββ=+- 0,1,...,i s = (5.2)
X 滞后项的系数值等额递减,从t X 的(1)s β+递减到t s X -的β。把(5.2)式代
入(5.1)式得到
[(1)]s
t i t i t
i s
t i t
i Y X s i X αβεαβε-=-==++=++-+∑∑ (5.3)
令
[(1)]s
t t i i Z s i X -==+-∑
这样方程(5.3)式表示为由被解释变量t Y 对常数项和t Z 回归估计得到。t Z 可由给定的s 和t X 计算得到。因此,我们可以把参数估计的任务从0β,1β,…,s
β减少到只有β一个。一旦得到?β,那么?i
β(0,1,...,i s =)就可以由(5.2)式计算得到。尽管这个过程很简单,但是这种滞后项的设定受到太多限制,所以实际上并不经常使用。
令(),0,1,...,i f i i s β==,如果()f i 是定义在一个闭区间上的连续函数,它可以由一个r 阶多项式来逼近,即
01()...r r f i i i ααα=+++ (5.4)
例如,如果2r =,那么
2
012i i i βααα=++ 0,1,2,...,i s =
所以,
00
1012
201224βαβαααβααα==++=++
…. … … …
2012
s s s βααα=++
一旦估计得到01,αα和2α,就可以计算得到0β,1β,…,s β。事实上,把
2012i i i βααα=++代入方程(5.1)式,我们可以得到
201202012000()s
t t i t
i s s
s
t i t i t i t
i i i Y i i X X iX i X ααααεααααε-=---====++++=++++∑∑∑∑ (5.5)
(5.5)式表明01,,ααα和2α可以由以t Y 为被解释变量,00
s t i i Z X -==
∑
、
10s
t i i Z iX -==∑以及220s
t i i Z i X -==∑为解释变量的回归估计得到。这个方法由
Almon (1965)提出并称为Almon 多项式法。
这里需要注意的是,应用该方法的问题是要选择s 和r ,即t X 的滞后项数和每个多项式的次数。Davidson 和MacKinnon (1993)建议,以回归方程(5.1)式为基础,首先确定合理的最大滞后值s *,使之与理论保持一致,然后考察随着s
*
的下降,方程的拟合度是否会下降。考察方程拟合度的一些可行标准包括:(i )最大化2R ;(ii )最小化AIC (Akaike, 1973),其中2/()(/)s T
AIC s RSS T e =;或
者(iii)最大化BIC ,其中/()(/)s T
BIC s RSS T T
=,RSS 代表残差平方和。2
R 、
AIC 和BIC 会给予较高的s 值一个惩罚,从而避免自由度的过度损失。多数回归软件如SHAZAM 、Eviews 和SAS 均提供上述统计值。
确定滞后长度s 值后,就可以进一步确定多项式的次数r 值。首先选择一个较高的r 值并按照(5.5)构造变量Z 。如果r =4是所选择的多项式最高次数,且
4440s
t i Z i X -==∑的系数4a 不显著,那么去除4Z ,并令3r =,重新运行回归,
如果3Z 的系数显著,则停止该过程,否则进一步降低r 值,令2r =,再重新运行回归直至停止。
研究者通常施加终端约束在Almon 滞后模型上。一个近终端约束是指(5.1)
式中的10β-=。这意味着在等式(5.5)中,这个终端约束对二次多项式中的α值
产生一个约束:1012(1)0f βααα-=-=-+=。这个约束使我们可以在给定
12,αα条件下求出0a 。事实上,构造012ααα=-代入(5.5)式,回归方程变为:
110220()()t t Y Z Z Z Z αααε=+++-+ (5.6)
这样,一旦估计得到1a 和2a ,就可以计算0a ,从而可以计算i β。这个约束
实际上表明1t X +对t Y 无影响。这可能并不是合理的假设,特别是在本章消费—收
入的例子中,其中下一年的收入将进入到恒久收入或终身收入中。当10s β+=时,一个更为合理的假设是远终端约束。
图5.2 具有终端约束的多项式滞后
这意味着(1)t s X -+对t Y 无影响。时间越早的变量,对当期的影响就越小。我们要做的就是要回溯到足够早,以使其对当期的影响不显著。这个远终端约束等同于把(1)t s X -+从等式中移走。而一些学者把()i f i β=施加在这些约束上,例如
1(1)0s f s β+=+=。当2r =时产生下面的约束:2012(1)(1)0a s a s a ++++=。
解得0a 后代入(5.5)式,约束回归方程变为:
2110220[(1)][(1)]t t Y Z s Z Z s Z αααε=+-++-++ (5.7)
我们也可以同时使用两个终端约束,把回归方程中要估计的三个a 值减少到一个。通过使回归方程中不包含1t X +和(1)t s X -+,可施加约束110s ββ-+==。然而,这个终端约束施加了一些额外的约束,即关于a 的多项式必须在1i =-和
(1)i s =+时经过0,如图5.2所示。
这些额外的约束可能是错的。换句话说,这个多项式可以与X 轴相交于其他
点而不是-1或(1)s +。施加这些约束,无论其是否是真的,都减少了估计量的方差,如果约束不是真的,则会产生偏倚。这从直觉上就可以看出,因为这些约束提供了额外的信息,这些信息可以提高估计的可信度。可以用均方误差标准来决定是否应施加这些限制,具体参见Wallace (1972)。一般说来,我们在使用这些约束必须非常小心,它们有时看起来是不合理的或无效的,因此必须进行正式检验,具体参见Schmidt and Waud (1975)。
§5.2 无穷分布滞后模型
5.2.1 柯依克(Koyck )模型
在§5.1节中,我们分析的是对t X 施加有限阶滞后。一些滞后有时是无穷阶的,例如,几十年前对高速公路和道路的投资可能在今天仍然对GDP 有影响。在这种情况下,我们把方程(5.1)式重新写成:
1
t i t i t i Y X αβε∞
-==++∑, 1,2,...,t T = (5.8)
用T 个观测值去估计无限个i β,唯一可行的方法是对i β施加更多结构。首先,我们标准化这些i β值,也即令/i i ωββ=,其中0
i i ββ∞==
∑
。如果所有这些i β值
有相同的符号,即与β的符号相同,且对所有的i 有01i ω≤≤和
1i i ω∞==∑
。这
意味着i ω可被视为概率值。Koyck (1954)对i ω施加了几何滞后,也即,
(1)i i ωλλ=-,0,1,...,i =∞。把(1)i i i ββωβλλ==-代入(5.8)式,可得
(1)i t t i t i Y X αβλλε∞
-==+-+∑ (5.9)
方程(5.9)式是Koyck 滞后的无穷滞后形式。t X 的一单位变化对t Y 的短期影响为(1)βλ-;另一方面,t X 一单位变化对t Y 的长期影响为
00i i i i ββωβ∞∞
====∑∑。Koyck 滞后结构暗示着随着时间推移,t X 的一单位变
化对t Y 的影响逐渐降低。例如,如果1/2λ=,那么0/2ββ=,1/4ββ=,
2/8ββ=等等。
定义1t t LX X -=,作为滞后算子,我们有i
t t i L X X -=,化简式(5.9)式,
得到
(1)()(1)/(1)i t t t
i t t
Y L X X L αβλλεαβλλε∞
==+-+=+--+∑ (5.10)
这里我们定义
1/(1)i
i c c ∞
==-∑
,把(5.10)式左右边都乘以(1)L λ-,可得 11(1)(1)t t t t t Y Y X λαλβλελε---=-+-+-
即有
11(1)(1)t t t t t Y Y X λαλβλελε--=+-+-+- (5.11)
这是无穷分布滞后的自回归形式,因为其把被解释变量t Y 的自回归项作为解释变量。注意到我们把估计无穷个i β值的问题简化为估计(5.11)式中的λ和β。然而,OLS 可能产生一个有偏和不一致的估计值,因为(5.11)式中包含了一个滞后因变量和序列相关的误差项。事实上在(5.11)式中的误差是一个一阶的移动平均过程,也即MA (1)。我们现在介绍两个类似式(5.11)的经济模型。
5.2.2 两类动态经济模型 一、适应性期望模型
适应性期望模型(Adaptive Expectations Model, AEM )是,假设产出t Y 是期望销售量t X 的函数,而后者是不可观测的,也即
t t t Y X αβε*=++ (5.12)
对模型(5.12)式中的期望销售量通过适应修正,即
11()t t t t X X X X δ***---=- (5.13)
即
1(1)t t t X X X δδ**-=+- (5.14)
说明(5.14)式是,t 期的销售量由1t -期的预期销售量和t 期时刻的实际销售量加权决定。
这里注意,式(5.14)式是一个误差学习模型,这个模型从过去经验中学习,并通过观测当期销售量调整期望值。使用滞后算子1()t t L X X -=,这样(5.14)
式可以写为
/[1(1)]t t X X L δδ*=-- (5.15)
通过(5.15)式,(5.12)式最后的表达为
/[1(1)]t t t Y X L αβδδε=+--+ (5.16)
式(5.16)式两边同乘以[1(1)]L δ--,可得
11(1)[1(1)](1)t t t t t Y Y X u δαδβδδε----=--++-- (5.17)
当(1)λδ=-时(5.17)式和式(5.11)式完全一致。
二、部分调整模型(Partial Adjustment Model, PAM ) 设部分调整模型(Partial Adjustment Model, PAM )为
t t Y X αβ*=+ (5.18)
其中,t X 为解释变量,模型(5.18)式中有一个不均衡的成本和一个向均衡调整的成本,也即
221()()t t t t Cost a Y Y b Y Y *-=-+- (5.19)
这里,t Y *
是Y 的目标或平衡水平,而t Y 是Y 的当期水平。式(5.18)的第一项给出了一个二次损失函数,其与t Y 和均衡水平t Y *
之间的距离成正比。第二个二次项代表了调整成本。最小化这个关于Y 的二次成本函数,我们得到
1(1)t t t Y Y Y γγ*-=+- (5.20)
其中/()a a b γ=+。注意到如果调整成本为0,那么0,1b γ==,目标立即实现。然而,由于存在调整成本,特别是在形成理想的资本存量时。因此,(5.18)式变为
1(1)t t t t Y X Y u γαγβγγ-=++-+ (5.21)
当(1)λγ=-时(5.21)式类似式(5.11)式,除了误差项不是MA(1)过程。
§5.3 序列相关动态模型的估计与检验
5.3.1 自回归模型的性质及序列相关检验
AEM 和PAM 方程都属于无穷分布滞后的自回归形式。在两种情况下,模型中都包含一个滞后的因变量和一个误差项,误差项在(5.11)式中是一阶移动平均的,在(5.21)式中是经典的或自回归的。在本节,我们将探讨这种自回归(autoregressive )或动态(dynamic )模型的估计与检验。
如果在回归方程中存在1t Y -,且t u 为经典扰动项,如式(5.21)中的情况,那么1t Y -与误差项t ε无同期相关。因此,扰动项满足经典线性回归的基本假设,有1()0t t E Y ε-=,同时有11()0t t E Y ε--≠。换句话说,1t Y -与当期扰动项t ε不相关,但与滞后扰动项1t ε-相关。在这种情况下,只要扰动项不是序列相关的,OLS 估计量将是有偏的,但仍然保持一致性和渐近有效性。但这种情况不大可能发生,因为经济数据多是存在趋势的宏观时序。更可能出现的情况是,t ε是序列相关的。在这种情形下,OLS 估计量将是有偏的和不一致的。直观上看,t Y 与t ε相关,1t Y -与1t ε-相关。如果t ε和1t ε-相关,那么t Y 就与1t Y -相关。这意味着这些滞后于Y 的
因变量都与t ε相关,因此我们面临一个内生性的问题。先让我们分析无常数项时用OLS 估计简单自回归模型会得到什么。
1t t t Y Y βε-=+,1β<,1,2,...,t T = (5.22)
其中1,
1t t t ερευρ-=+<,t υ~2(0,)IIN υσ。容易证明,
22
11112222?//T
T
T
T
OLS
t t t t t t t t t t YY Y Y Y ββε----======+∑∑∑∑ (5.23)
其中lim()OLS p asymp ββ-=。2bias()(1)/(1)OLS βρβρβ=-+。该渐近的偏倚当0ρ>时是正的,当0ρ<时是负的。同时,当β值减小或ρ值增大时,该渐近的偏倚会增大。例如,若0.9,0.2ρβ==,β的渐近偏倚为0.73,是β值的
三倍多。同理21122???/T
T t t t t t Y ρ
εε--===∑∑,1??t t OLS t Y Y εβ-=-时, 2??lim()(1)/(1).()OLS
p asymp bias ρρρβρββ-=--+=- (5.24) 这意味着如果0ρ>,那么ρ将有负的偏倚。反之,如果0ρ<,那么ρ将有正的偏倚。在这两种情况下,ρ都是有偏的,与实际值相比会更趋近于0。可
以进一步发现,D.W.统计量的渐近偏倚是?OLS
β渐近偏倚的两倍。这意味着D.W.统计量是有偏的,且较不容易拒绝无序列相关的零假设。因此,如果D.W.统计量拒绝0ρ=的零假设,那么我们将有更大的把握确认拒绝零假设,并确信序列相关的存在。另一方面,如果没有拒绝零假设,那么不能完全相信D.W.统计量的判断,而应该采用另一个关于序列相关的检验,也即Durbin (1970)提出的,存在一个滞后因变量时应采用的Durbin h 检验。应用式(5.11)和式(5.21)计算OLS
估计量,忽略其可能产生的偏倚,并应用所得到的残差计算ρ,Durbin h 统计量由下式给出:
1/21?[/(1var(.))]t h n n coeff of Y ρ
∧
-=- (5.25) 在0ρ=的零假设下,其渐近分布为(0,1)N 。如果1[var(.)]t n coeff ofY ∧
-比1大,那么h 检验无法进行。Durbin 提出一个补救方法,将OLS 的残差t e 对1t e -和模型中自变量(包括滞后的因变量)做回归,并检验1t e -的系数是否显著。事实上,这个检验可以扩展至更高阶的自回归误差。假设t ε服从()AR p 过程
1122...t t t p t p t ερερερευ---=++++ (5.26)
该检验是由t e 对12,,...,t t t p e e e ---以及1t Y -回归。这个检验的零假设是
012;..0p H ρρρ====,检验统计量为2TR ,其分布为2
p χ。该检验称为拉格
朗日乘子检验,由Breusch (1978)和Godfrey (1978)各自独立提出。事实上,这个检验还有其他用途,如检验扰动项是否存在()AR p 或()MR p 结构。Kiviet (1986)指出,尽管该检验适用于大样本,但即使在小样本中,Breusch Godfrey 检验也比Durbin h 检验更具优势。
5.3.2包含(1)AR 扰动项的滞后因变量模型
一个包含滞后因变量和自回归误差项的模型可采用工具变量法(instrumental variables ,IV )来估计。简而言之,工具变量通过用1t Y -的预期值1t Y -代替1t Y -来
校正1t Y -与误差项之间的相关性。1t Y -通过1t Y -对一些外生变量回归以获得,将这些外生变量称为一组Z 变量,这组Z 变量称为1t Y -的工具变量。因为这些变量是外生的且与t ε不相关,所以1t Y -与t ε不相关。假定回归方程为
1t t t t Y Y X βεαγ-=+++, 2,...,t T = (5.27)
找到至少一个外生变量t Z 作为1t Y -的工具变量,将1t Y -对,t t X Z 和常数项做回归,可得
11123??????t t t t t t Y Y v Z X v ααα--=+=+++ (5.28) 那么1
123????t t t Y Z X ααα-=++,且独立于t ε,因为它是外生变量的线性组合。但1t Y -和t ε相关。这意味着?t v 是1t Y -的一部分且与t ε相关。将11
??t t t Y Y v --=+代入(5.27)式,我们可得
1??()t t t t
t Y Y X v αβγεβ-=++++ (5.29) 1t Y -与新的误差项t t v εβ+不相关,因为在(5.28)式中有10t t Y v -=∑。另
一方面,我们假设t X 与t ε也不相关,从(5.28)式中我们知道t X 也满足
0t t
X v
=∑。因此,t X 与新的误差项t t v εβ+不相关。这意味着应用OLS 估计
(5.29)式中会得到,αβ和γ的一致估计量。
因此,要解决的问题是去哪里找工具变量t Z 。这个t Z 必须满足:(i )与t ε不
相关。(ii )较好地预测1t Y -,但并不能完全预测1t Y -,除非11?t t Y Y --=。如果11?t t Y Y --=,
就等于回到OLS ,也就丧失了一致性。(iii )
2
/t
z
T ∑必须是有限的且不为零。重
新定义t t z Z Z =-。在这种情况下,1t X -似乎是天然的可供选择的工具变量:它是外生变量且能够较好地预测1t Y -,满足
2
1/t X T -∑是有限的且不为零。
换句话说,令1t Y -对常数项、1t X -和t X 回归,可得到1t Y -。以t X 的滞后项作为工具变量,可以改进估计的小样本性质。在(5.29)式中引入1t Y -,可以获得回归参数的一致估计量。Wallis (1967)在原方程(5.29)中引入一致性估计量,并获得残差t ε,然后计算得到
2121?[/(1)]/[/](3/)T T
t t t t t T T T ρ
εεε-===-+∑∑ (5.30) 最后一项校正了?ρ
的偏倚。我们可以用式(5.27)估计得到的?ρ而非ρ进行Pr ais Winsten -的广义最小二乘估计,参见Fomby 和Guilkey (1983)
。 另一个可供选择的两步法是由tan Ha aka (1974)提出的。在估计出(5.29)
和从(5.27)中获得残差t ε后,tan Ha aka (1974)建议由1t t t Y Y Y ρ*
-=-对
112t t t Y Y Y ρ*---=-,1t t t X X X ρ*
-=-和1t t ε-回归。注意这是一个
Cochrane Orcutt -变换,它忽略了第一个观测值。同理,
2133/T T
t t t t t t t t ρεεε-===∑∑也忽略了由Wallis (1967)提出的小样本偏差校正因
素。令δ为1t t ε-的系数回归值,那么
ρ的有效估计量由ρρδ=+给出。
tan Ha aka 指出,正态分布条件下,该估计结果与最大似然法的估计结果渐近相
等。
5.3.3包含MA (1)扰动项的滞后因变量模型
ln Zel er 和Geisel (1970)估计出了由(5.11)式给出的无穷分布滞后的
Koyck 自回归模型。AEM 模型也有类似的设定。它是一个包含滞后因变量和MA
(1)误差项的回归模型,且误差项包含一个附加的约束,那就是1t Y -的系数与MA (1)参数相同。为简化分析,假设为
11()t t t t t Y Y X αλβελε--=+++- (5.31)
令t t t Y ωε=-,(5.31)式变成
1t t t X ωαλωβ-=++ (5.32)
在(5.32)式中连续替代t ω的滞后值,得到
211011(1...)(...)
t t t t t t X X X ωαλλλλωβλλ---=+++++++++
(5.33)
针对(5.33)式,用(t t Y ε-)替代t ω,得到
211011(1...)(...)t t t t t t t Y X X X αλλλλωβλλε---=++++++++++
(5.34)
若已知λ,在假设扰动项无序列相关时,可应用OLS 方法估计该式。但λ未
知,Zellner 和Geisel (1970)提出了一个估计λ(其中01λ<<)的方法。令残差平方和最小化可得到最优λ,相应的回归给出了,αβ和0ω的估计值。最后一个参数000Y u ω=-可视为因变量初始观测值的预期值。
Klein (1958)考察了一个无限Koyck 滞后的直接估计量,设定为(5.9)式,得到(5.34)式。对λ的搜索可得到参数的最大似然估计量。然而,注意到0ω的估计量不是一致的。当t 趋向于无穷大,t
λ趋向于0,意味着没有新的信息来估计
0ω。事实上,一些应用研究者忽略了(5.34)式中的回归中的变量t λ,这么做可
能会存在问题,根据Maddala 和Kao (1971)和Schmidt (1975)的Monte Carlo 模拟,即使T=60或100,仍不应忽略(5.34)式中的t
λ。
总之,我们已经学会如何估计一个带有滞后因变量和序列相关误差项的动态模型。假设其误差项存在一阶自回归,本章论述了实现Wallis 两步估计法和Hatanka 两阶段法的基本步骤。对于误差项存在一阶移动平均的情况,本章论述实现Zellner-Geisel 法的基本步骤。
§5.4 自回归分布滞后模型
本章的前两节分别考虑了解释变量存在有限分布滞后,以及包含因变量一阶滞后和解释变量当前值的自回归模型。通常,自回归分布滞后模型可应用于解释更一般的经济关系。最简单的设定是ADL (1,1)模型:
1011t t t t t Y Y X X αλββε--=++++ (5.35)
其中t Y 和t X 都有一阶滞后。通过对t Y 和t X 设定更高阶的滞后,可定义ADL (p,q )模型,即对t Y 取p 阶滞后,对t X 取q 阶滞后。我们可以检验该设定是否足够一般化以保证扰动项服从白噪音。这样我们可以检验是否应施加一些约束,如减少滞后的阶数以得到一个更简单的模型,或估计一个更简单的静态模型,并用Cochrane Orcutt -校正序列相关。
这个一般化的建模过程由David Hendry 提出,并且通过计量软件PC Give -来实现,参见Gilbert (1986)。
现考虑(5.35)式中的ADL (1,1)模型,转换为自回归形式:
222011(1...)(1...)()t t t t Y L L X X αλλλλββε-=+++++++++ (5.36)
其中
1λ<。该方程可分析t X 的一单位变化对t Y 未来值的影响,有
0/t t Y X β??=,110/t t Y X βλβ+??=+等等,即给出了Y 对X 的短期响应,而长
期响应是这些偏导数之和,等于01()/(1)ββλ+-。也可以从(5.36)式导出,设
长期静态平衡为(,)t t Y X **
,其中1t t t Y Y Y *-==,1t t t X X X *-==,且假设扰动项
为0,即
0111Y X ββα
λ
λ
**
+=
+
-- (5.37)
在(5.35)式中,用1t t Y Y -+?代替t Y ,用1t t X X -+?代替t X ,得到
01011(1)()t t t t t Y X Y X αβλββε--?=+?--+++
可重新写为
01
011(1)[]11t t t t t Y X Y X ββα
βλελ
λ
--+?=?---
-
+-- (5.38)
注意在括弧中的项包含了来自(5.37)式的长期均衡参数。事实上,括弧中的项代表了与1t X -相应的1t Y -对长期均衡的偏离。方程(5.38)称为误差修正模型(Error Correction Model ,ECM ),参见Davidson, Hendry, Srba 和Yeo (1978)。通过1t Y -加上t X 变化的短期影响,以及长期均衡调整项,可获得t Y 。因为扰动是白噪音,这个模型可用OLS 估计。
§5.5 实证分析
我们应用美国总统经济报告1950-1993年的消费—收入数据的回归,参见表5.1。
表5.1 具有算术滞后约束的回归
我们估计一个消费—收入回归方程并令收入取滞后五期。方程(5.1)中的所有变量均取对数值,且5s =。表5.1给出了SAS 的输出结果,回归方程施加了式(5.2)的线性算术滞后(linear arithmetic lag )。
注意到SAS 输出结果中,5t Y -的系数为0.047β=,5t Y -在表中由5YLAG 表示。在5%显著性水平下,t 值为83.1,统计显著。4t Y -的系数为2β,在表中由
4YLAG 代表,其余以次类推。t Y 的系数60.281β=。在回归表格的底部,SAS
分别检验了5个系数的约束。我们可以发现由三个约束在5%显著性水平下拒绝零假设。我们可以用F-检验对算术滞后(arithmetic lag )进行联合假设检验。无约束残差平方和(The Unrestricted Residual Sum of Squares,URSS )可通过t C 对常数项和15,,...,t t t Y Y Y --回归得到,URSS=0.00667。约束的残差平方和RRSS 由表1给出,为0.01236,它施加了式(2)中的5个约束。因此,
(0.012360.00667)/5
5.4597
0.00667/32F -=
=
在零假设下,其分布为5,32F 。观察到的F 统计量的p 值为0.001,我们拒绝了线性算术滞后的约束。
接下来我们施加(5.5)式中的二次多项式Almon 滞后假设。表2给出了5s =且施加了近终端约束的SAS 输出结果。在这种情况下,估计得到的回归参数值先
上升而后下降:
0150.193,0.299,...,0.159βββ===-。只有5β统计不显著。
此外,SAS 报告了对于近终端约束的t 检验结果,拒绝假设的p 值为0.0001。Almon 滞后约束的联合检验也可以采用Chow ’s F 统计量。URSS 由t C 对15,,...,t t t Y Y Y --和常数项回归得到,URSS=0.00667。
表5.2 Almon 多项式滞后,r=2,s=5且施加近终端约束
PDLREG Procedure Dependent Varible =C
表5.2给出RRSS 的值为0.014807,包含了4个约束。因此,
@计量经济学主要公式
序 公式名称计算公式 号 y t = β0 + β1 x t + u t 1真实的回归模 型 2估计的回归模 型y t =+x t + 3真实的回归函 E(y t) = β0 + β1 x t 数 4估计的回归函 数=+x t 5最小二乘估计 公式 6 和的方 差 7σ2的无偏估 计量= s2 = 8 和估计 的方差 9总平方和 ∑(y t -) 2 10回归平方和 ∑(-) 2 11误差平方和 ∑(y t -)2 = ∑()2 12可决系数(确 定系数) 13检验β0,β1 是 否为零的t统 计量
14β1的置信区间 -tα(T-2) ≤β1≤+tα(T-2) 15单个y T +1的点 预测=+x T+1 16E(y T+1)的区间 预测 17单个y T+1的区 间预测 18样本相关系数 表3.4 多元线性回归模型的主要计算公式 序号公式名称计算公式 1 真实的回归模型Y= X β+ u 2 估计的回归模型Y = X+ 3 真实的回归函数E(Y) = X β 4 估计的回归函数= X 5 最小二乘估计公式= (X 'X)-1X 'Y 6 回归系数的方差Var() = σ2(X 'X)-1 7 σ2的无偏估计量= s2 ='/ (T - k) 8 回归系数估计的方差() =(X 'X)-1 9 回归平方和SSR = = '- T 10 总平方和SST = Y 'Y - T 11 残差平方和SSE = ' 12 可决系数 13 调整的可决系数
14 F统计量 15 t统计量 16 点预测公式 C = (1 x T+1 1 x T+1 2… x T+1 k-1 ) = C = 0 +1 x T+1 1 + … + k-1 x T+1 k-1 17 E(y T+1) 的置信区间预 测 C±tα/2 (1, T-k)s 18 单个y T+1的置信区间预 测 C±tα/2 (T-k)s 19 预测误差e t = - y t, t= 1, 2, …, T 20 相对误差PE = , t= 1, 2, …, T 21 误差均方根 22 绝对误差平均 23 相对误差绝对值平均 24 Theil系数 25 偏相关系数是控制z t不变条件下的x t, y t的简单相关系数。 26 y t与x t1,x t2,…,x tk–1的 复相关系数 是y t与的简单相关系数。其中是y t对x t1,x t2,…x tk–1 回归的拟合
计量经济学的概念
计量经济学是经济科学领域内的一门应用科学,以一定的经济理论和实际统计资料为基础,运用数学、统计方法与计算机技术,以建立经济计量模型为主要手段,定量分析研究具有随机特性的经济变量关系。 2、数理经济模型与计量经济模型的区别。 数理:揭示经济活动中各个因素之间的理论关系,用确定性的数学方程加以描述。 计量:揭示经济活动中各个因素之间的定量关系,用随机性的数学方程加以描述。 3、经典计量经济学模型的一般形式。 4、计量经济学的数据类型。 时间序列数据:按时间先后排列的统计数据。 截面数据:一个或多个变量在某一时点上的数据集合。 合并数据(平行数据):既包含时间序列数据又有截面 数据。 5、建立计量经济学模型的步骤。 1) 模型的数学形式。③拟定模型中待估计参数的理论期望 值。 2)样本数据的收集: 差项产生序列相关。②截面数据易引起模型随机误差项 产生异方差。③样本数据的质量:完整性、准确性、可 比性、一致性。 3)模型参数的估计。 4 度检验、变量的显着性检验、方程的显着性检验。③计 量经济学检验:序列相关、异方差法(随机误差项)、 多重共线性(解释变量)④模型预测检验。 6、计量经济学模型的应用。 1)结构分析;2)经济预测;3)政策评价;4)检验与发展经济理论。 7、如何正确选择解释变量。 作为“变量”的原因:1 2)考虑数据的可得性;3)考虑入选变量之间的关系。 8、回归分析的目的。 1)根据自变量的取值,估计应变量的均值;2)检验建立在经济理论基础上的假设;3) 值,预测应变量的均值。 9、总体回归函数(PRF)和样本回归函数(SRF)各变量系数名称及函数方程。 10、随机误差项(Ui)的性质或主要内容。
经典单方程计量经济学模型多元线性回归模型
第三章、经典单方程计量经济学模型:多元线性回归模型 一、内容提要 本章将一元回归模型拓展到了多元回归模型,其基本的建模思想与建模方法与一元的情形相同。主要内容仍然包括模型的基本假定、模型的估计、模型的检验以及模型在预测方面的应用等方面。只不过为了多元建模的需要,在基本假设方面以及检验方面有所扩充。 本章仍重点介绍了多元线性回归模型的基本假设、估计方法以及检验程序。与一元回归分析相比,多元回归分析的基本假设中引入了多个解释变量间不存在(完全)多重共线性这一假设;在检验部分,一方面引入了修正的可决系数,另一方面引入了对多个解释变量是否对被解释变量有显著线性影响关系的联合性F检验,并讨论了F检验与拟合优度检验的内在联系。 本章的另一个重点是将线性回归模型拓展到非线性回归模型,主要学习非线性模型如何转化为线性回归模型的常见类型与方法。这里需要注意各回归参数的具体经济含义。 本章第三个学习重点是关于模型的约束性检验问题,包括参数的线性约束与非线性约束检验。参数的线性约束检验包括对参数线性约束的检验、对模型增加或减少解释变量的检验以及参数的稳定性检验三方面的内容,其中参数稳定性检验又包括邹氏参数稳定性检验与邹氏预测检验两种类型的检验。检验都是以F检验为主要检验工具,以受约束模型与无约束模型是否有显著差异为检验基点。参数的非线性约束检验主要包括最大似然比检验、沃尔德检验与拉格朗日乘数检验。它们仍以估计无约束模型与受约束模型为基础,但以最大似然 χ分布为检验统计原理进行估计,且都适用于大样本情形,都以约束条件个数为自由度的2 量的分布特征。非线性约束检验中的拉格朗日乘数检验在后面的章节中多次使用。 二、典型例题分析 例1.某地区通过一个样本容量为722的调查数据得到劳动力受教育的一个回归方程为36 .0 . + = - 10+ 094 medu fedu .0 sibs edu210 131 .0 R2=0.214 式中,edu为劳动力受教育年数,sibs为该劳动力家庭中兄弟姐妹的个数,medu与fedu分别为母亲与父亲受到教育的年数。问
经典计量经济学应用模型
经典计量经济学应用模型 一、单选题 1. 生产函数的要素边际替代率表示的是( )。 A .维持产出不变,增加一单位的某一要素投入,需增加另一要素投入数量 ; B. 维持产出不变,减少一单位的某一要素投入,需增加另一要素投入数量; C .要素K 对要素L 的边际替代率等于ln()/ln()L K MP K d d L MK ; D .要素的边际替代率是要素的替代弹性。 2. 两种生产要素的比例的变化率与边际技术替代率的变化率之比叫做 ( )。 A .要素的替代弹性 B. 要素的产出弹性 C .边际技术替代率 D .技术进步率 3. 下列生产函数中,要素的替代弹性为变量的是( ) A .线性生产函数 B. VES 生产函数 C .C D -生产函数 D .CES 生产函数 4. 下列生产函数中,要素的替代弹性为∞的是( ) A .线性生产函数 B. 投入产出生产函数 C .C D -生产函数 D .CES 生产函数 5. 下列生产函数中,要素的替代弹性分别为0和1的是( ) A .线性生产函数和C D -生产函数 B. 投入产出生产函数和C D -生产函数 C .C D -生产函数和线性生产函数 D .CES 生产函数和投入产出生产函数 6. 狭义技术进步是指( )。 A .生产水平的提高 B. 产品价格的提高 C .要素质量的提高 D .管理水平的提高 7. 在C D -生产函数Y AL K αβ=中( )。 A .α和β是产出弹性 B. α和β是边际产出 C .α和β是替代弹性 D .A 是要素替代弹性
8. CES 生产函数/12()m Y A K L ρρρδδ---=+中,01ρ<<,1δ越接近于1,表示 ( )。 A .资本密集度越高 B. 资本密集度越低 C .技术进步程度越高 D .技术进步程度越高 9. 中性技术进步中,希克斯中性进步指的是( )。 A .要素之比/K L 不随时间变化 B. 劳动产出率/Y L 不随时间变化 C .自资本产出率/Y K 不随时间变化 D .资本密集度/L K E E ω=随技术 进步变大 10.当需求完全无弹性时,表示( ) A .价格与需求量之间存在完全线性关系 B.价格上升速度与需求量下降速度相等 C .无论价格如何变动,需求量都不变 D .价格上升,需求量也上升 11. 关于扩展的线性支出系统需求函数模型: (),1,2,,i i i j j j i b q r I p r i n p =+-=∑L 下列说法不正确的是( ) A .j γ是第j 种商品的基本需求量 B.i b 是第i 种商品的边际消费向 C .()j j j I p r -∑是剩余收入用于购买第j 种商品的支出 D .1i i b ≤∑ 12. 直接效用函数蒋孝勇表示为下列哪一项的函数( )。 A .商品供应量 B. 商品需求量 C .商品价格 D .收入 13. 消费函数模型的一般形式为( )。 A .t t t C Y αβμ=++ B. 011t t t C Y C ββμ-=++ C .1(,)t t t t C f Y C μ-=+ D .1(,)t t t t C f Y Y μ-=+ 14.下面四种单方程需求模型中,不能用于分析价格队需求量影响的模型时 ( )。 A .线性需求函数模型 B. 对数线性需求函数模型 C .耐用品消费调整模型 D .状态调整模型
计量经济学第二章主要公式
第二章主要公式 资料地址:https://www.360docs.net/doc/d51289509.html,/jl 1、回归模型概述 (1)相关分析与回归分析 经济变量之间的关系:函数关系、相关关系 相关关系:单相关和复相关,完全相关、不完全相关和不相关,正相关与负相关,线性相关和负相关,线性相关和非线性相关。 相关分析: ——总体相关系数XY ρ= ——样本相关系数()() n i i XY X X Y Y r --= ∑ ——多个变量之间的相关程度可用复相关系数和偏相关系数度量 回归分析:相关关系 + 因果关系 (2)随机误差项:含有随机误差项是计量经济学模型与数理经济学模型的一大区别。 (3)总体回归模型 总体回归曲线:给定解释变量条件下被解释变量的期望轨迹。 总体回归函数:(|)()i i E Y X f X = 总体回归模型:(|)()i i i i i Y E Y X f X μμ=+=+ 线性总体回归模型:011,2,...,i i i Y X i n ββμ=++= (4)样本回归模型 样本回归曲线:根据样本回归函数得到的被解释变量的轨迹。 (线性)样本回归函数: 01???i i Y X ββ=+ (线性)样本回归模型:01???i i i Y X e ββ=++ 2、一元线性回归模型的参数估计 (1)基本假设 ① 解释变量:是确定性变量,不是随机变量 var()0i X = ② 随机误差项:零均值、同方差,在不同样本点之间独立,不存在序列相关等 ()01,2,...,i E i n μ== 2var()1,2,...,i i n μσ==
cov(,)0;,1,2,...,i j i j i j n μμ=≠= ③ 随机误差项与解释变量:不相关 cov(,)01,2,...,i i X i n μ== ④ (针对最大似然法和假设检验)随机误差项: 2~(0,)1,2,...,i N i n μσ= ⑤ 回归模型正确设定。 【前四条为线性回归模型的古典假设,即高斯假设。满足古典假设的线性回归模型称为古典线性回归模型。】 (2)参数的普通最小二乘估计(OLS ) 目标:21 min n i i e =∑ 对于一元线性回归模型:011,2,...,i i i Y X i n ββμ=++= 正规方程组: 011 011 ?? 2[()]0??2[()]0n i i i n i i i i Y X X Y X ββββ==?--+=????--+=??∑∑ 解得: 011 112 211??()()?()n n i i i i i i n n i i i i Y X X X Y Y x y X X x βββ====?=-???--?==??-?? ∑∑∑∑ (3)最大似然估计(ML ) 对于一元线性回归模型:011,2,...,i i i Y X i n ββμ=++= 重要的基本假设: 2~(0,)1,2,...,cov(,)0;,1,2,...,var()01,2,...,i i j i N i n i j i j n X i n μσμμ?=? =≠=?? ==? 得到:2 01~(,)1,2,...,i i Y N X i n ββσ+= 【且cov(,)0;,1,2,...,i j Y Y i j i j n =≠=,这个对最大似然法的估计很重要】 则目标:12,,...,n Y Y Y 的联合概率密度最大,即
计量经济学习题与解答
第五章经典单方程计量经济学模型:专门问题 一、内容提要 本章主要讨论了经典单方程回归模型的几个专门题。 第一个专题是虚拟解释变量问题。虚拟变量将经济现象中的一些定性因素引入到可以进行定量分析的回归模型,拓展了回归模型的功能。本专题的重点是如何引入不同类型的虚拟变量来解决相关的定性因素影响的分析问题,主要介绍了引入虚拟变量的加法方式、乘法方式以及二者的组合方式。在引入虚拟变量时有两点需要注意,一是明确虚拟变量的对比基准,二是避免出现“虚拟变量陷阱”。 第二个专题是滞后变量问题。滞后变量包括滞后解释变量与滞后被解释变量,根据模型中所包含滞后变量的类别又可将模型划分为自回归分布滞后模型与分布滞后模型、自回归模型等三类。本专题重点阐述了产生滞后效应的原因、分布滞后模型估计时遇到的主要困难、分布滞后模型的修正估计方法以及自回归模型的估计方法。如对分布滞后模型可采用经验加权法、Almon多项式法、Koyck方法来减少滞项的数目以使估计变得更为可行。而对自回归模型,则根据作为解释变量的滞后被解释变量与模型随机扰动项的相关性的不同,采用工具变量法或OLS法进行估计。由于滞后变量的引入,回归模型可将静态分析动态化,因此,可通过模型参数来分析解释变量对被解释变量影响的短期乘数和长期乘数。 第三个专题是模型设定偏误问题。主要讨论当放宽“模型的设定是正确的”这一基本假定后所产生的问题及如何解决这些问题。模型设定偏误的类型包括解释变量选取偏误与模型函数形式选取取偏误两种类型,前者又可分为漏选相关变量与多选无关变量两种情况。在漏选相关变量的情况下,OLS估计量在小样本下有偏,在大样本下非一致;当多选了无关变量时,OLS估计量是无偏且一致的,但却是无效的;而当函数形式选取有问题时,OLS估计量的偏误是全方位的,不仅有偏、非一致、无效率,而且参数的经济含义也发生了改变。在模型设定的检验方面,检验是否含有无关变量,可用传统的t检验与F检验进行;检验是否遗漏了相关变量或函数模型选取有错误,则通常用一般性设定偏误检验(RESET检验)进行。本专题最后介绍了一个关于选取线性模型还是双对数线性模型的一个实用方法。 第四个专题是关于建模一般方法论的问题。重点讨论了传统建模理论的缺陷以及为避免这种缺陷而由Hendry提出的“从一般到简单”的建模理论。传统建模方法对变量选取的
计量经济学考试必备公式大纲
学习用途,考试专用,请用完删除自己总结1159952047 1、异方差性:对于不同的样本点,随机干扰项的方差不再是常数,而是互不相同,则认为出现了异方差性。类型:单调递增型,单调递减型,复杂型。原因:⑴模型中遗漏了随时间变化影响逐渐增大的因素。(即测量误差变化)⑵模型函数形式设定误差。⑶随机因素的影响。(即截面数据中总体各单位的差异)后果:1.参数估计量非有效2.变量的显著性检验失去意义3.模型的预测失效检验:图示检验法,戈德菲尔德-匡特检验,怀特检验,帕克检验和戈里瑟检验处理:变异方差为同方差,或尽量缓解方差变异的程度。(加权最小二乘法(WLS),异方差稳健标准误法) 2、序列相关性:如果模型的随机干扰项违背了相互独立的基本假设,则称为存在... 原因:经济数据序列惯性;模型设定的偏误;滞后效应;蛛网现象;数据的编造后果:1.参数估计量非有效;2.变量的显著性检验失去意义;3.模型的预测失效检验方法:图示法;回归检验法;D.W.检验法;拉格朗日乘数检验补救方法:广义最小二乘法(GLS),广义差分法,随机干扰项相关系数的估计,广义差分法在计量经济学软件中的实现,序列相关稳健标准误法。 3、多重共线性:如果模型的解释变量之间存在着较强的相关关系,则称模型存在多重共线性。 原因:经济变量相关的共同趋势、滞后变量的引入、样本资料的限制后果(一)完全:1、参数估计值不确定。 2、参数估计值的方差会无限大。( 二)不完全:1、有可能求出参数的估计值,但估计值很不稳定。2、参数估计值的方差会随多重共线性(近似)程度的提高而增大。3、对总体参数的区间估计将会降低精确度(置信区间变宽)。评价区间估计的两个标准: (1)估计的可靠度。(2)估计的精确度 .4、对总体参数的显著性检验(t检验)在统计上将会不显著。检验:1.检验多重共线性是否存在2.判明存在多重共线性的范围克服方法:1.排除引起共线性的变量2.差分法3.见笑参数估计量的方差 4、●经典假定:1、零均值假定。2、同方差假定。3、无自相关假定。4、解释变量与随机误差项不相关。 5、无多重共线性假定。 6、正态性假定。●多元线性回归模型的基本假定:零均值假定、同方差和无自相关(条件方差不变、条件自相关等于0)、随机扰动项与解释变量不相关、无多重共线性、正态性假定独立同分布,且~ N (0,σ2) 5、拟和直线的优度-判定系数r2。TSS为总离差平方和,反映Y的样本观测值的平均差异程度;ESS 为Y的估计值与均值的离差平方和,反映解释变量的变化所引起的对Y的波动大小,即解释变量在模型中存在的重要程度;RSS为残差平方和,反映Y依据回归直线没有得到解释的变差。 6、F检验的意义(1)检验的不足。尽管具有对模型整体拟合状况的判断,但它并不能得到到底要多大时回归方程才算通过了拟合优度检验。虽然R2能够给出评价模型拟合好坏的度量,但它只是对样本的拟合程度进行评价,不能回答总体的真实状况。(2)F检验的目的。对于总体多元线性回归模型,从整体上看,多个解释变量与被解释变量之间是否存在显著的线性关系,或者说 Y 的变动是否依赖于这些解释变量的变化。由F统计量的构成可以看出(ESS服从自由度为k-1,RSS服从n-k 的分布),如果ESS显著地大于RSS,则表明不能认为所有的全为零,这时在很大程度上要拒绝。则在该意义下,说明回归方程中的所有解释变量对应变量存在显著性影响。F 检验的一般步骤是:(1)构造 F 统计量,即。(2)给定显著性水平,查F分布表,得临界值,其中k为参数的个数,n为样本容量。(3)比较判断。若F﹥,则拒绝原假使,表明回归函数从整体上看是显著的,即所有解释变量对应变量有显著性影响。 7、t 检验在多元线性回归模型里与一元的情况是一致的。需要注意的是在多元线性回归模型对参数的 t 检验中,即~ t(n-k) (在成立下)这里是服从自由度为 (n-k) 的 t 分布。因此,在多元的情况下,运用 t 检验的操作过程如下(1)提出假设(2)构造检验统计量在H 0 成立的情况下,有:~t(n-k)(3)计算t统计量值,。(4)根据t分布,给定显著性水平,查表得临界值。(5)比较判断,若,则拒绝 H 0 ,同时接受 H 1 。表明第 j 个解释变量 X j 对被解释变量 Y 存在显著性影响;否则,表明第 j 个解释变量 X j 对被解释变量 Y 不存在显著性影响。 8、
现代计量经济学模型体系解析
#学术探讨# 现代计量经济学模型体系解析* 李子奈刘亚清 内容提要:本文对现代计量经济学模型体系进行了系统的解析,指出了现代计量经济学的各个分支是以问题为导向,在经典计量经济学模型理论的基础上,发展成为相对独立的模型理论体系,包括基于研究对象和数据特征而发展的微观计量经济学、基于充分利用数据信息而发展的面板数据计量经济学、基于计量经济学模型的数学基础而发展的现代时间序列计量经济学、基于非设定的模型结构而发展的非参数计量经济学,并对每个分支进行了扼要的描述。最后在/交叉与综合0的方向上提出了现代计量经济学模型理论的研究前沿领域。 关键词:经典计量经济学时间序列计量经济学微观计量经济学 一、引言 计量经济学自20世纪20年代末30年代初诞生以来,已经形成了十分丰富的内容体系。一般认为,可以以20世纪70年代为界将计量经济学分为经典计量经济学(Classical Econometrics)和现代计量经济学(Mo dern Eco no metr ics),而现代计量经济学又可以分为四个分支:时间序列计量经济学(Tim e Ser ies Econo metrics)、微观计量经济学(M-i cro-econometrics)、非参数计量经济学(Nonpara-m etric Econometrics)以及面板数据计量经济学(Panel Data Eco nom etrics)。这些分支作为独立的课程已经被列入经济学研究生的课程表,独立的教科书也已陆续出版,应用研究已十分广泛,标志着它们作为计量经济学的分支学科已经成熟。 据此提出三个问题:一是经典计量经济学的地位问题。既然现代计量经济学模型体系已经成熟,而且它们都是在经典模型理论的基础上发展的,那么经典模型还有应用价值吗?是不是凡是采用经典模型的研究都是低水平和落后的?二是现代计量经济学的各个分支的发展导向问题。即它们是如何发展起来的?三是现代计量经济学进一步创新和发展的基点在哪里?回答这些问题,对于正确理解计量经济学的学科体系,对于计量经济学的课程设计和教学内容安排,对于正确评价计量经济学理论和应用研究的水平,对于进一步推动中国的计量经济学理论研究,都是十分有益的。 现代计量经济学的各个分支是以问题为导向,以经典计量经济学模型理论为基础而发展起来的。所谓/问题0,包括研究对象和表征研究对象状态和变化的数据。研究对象不同,表征研究对象状态和变化的数据具有不同的特征,用以进行经验实证研究的计量经济学模型既然不同,已有的模型理论方法不适用了,就需要发展新的模型理论方法。按照这个思路,就可以用图1简单地描述经典计量经济学模型与现代计量经济学模型各个分支之间的关系。 本文试图从方法论的角度对现代计量经济学模型的发展,特别是现代计量经济学模型与经典计量经济学模型之间的关系进行较为系统的讨论,以期对未来我国计量经济学的发展研究提供借鉴和启示。本文的内容安排如下:首先分析经典计量经济学模型的基础地位,明确它在现代的应用价值,同时对发生于20世纪70年代的/卢卡斯批判0的实质进行讨论;然后依次讨论时间序列计量经济学、微观计量经济学、非参数计量经济学以及面板数据计量经济学的发展,回答它们是以什么问题为导向,以什么为目的而发展的;最后以/现代计量经济学模型体系的分解与综合0为题,讨论现代计量经济学的前沿研究领域以及从对我国计量经济学理论的创新和发展 ) 22 ) *本文受国家社会科学基金重点项目(08AJY001,计量经济学模型方法论基础研究)的资助。
第五章-单方程计量经济学应用模型试题及答案
第五章 单方程计量经济学应用模型 一、填空题: 1.当所有商品的价格不变时,收入变化1%所引起的第i 种商品需求量的变化百分比叫做需求的 。 2.对于生活必需品,需求的收入弹性i E 的取值区间为 ,需求的自价格弹性的取值区间为 。 3.当收入和其他商品的价格不变时,第j 种商品价格变化1%所引起的第i 种商品需求量的变化百分比,叫做需求的 。 4.替代品的需求互价格弹性ij E 0;互补品的需求互价格弹性 ij E 0;无关商品的需求 互价格弹性 ij E 0。 5.吉芬商品的需求自价格弹性 0。 6.西方国家发展的需求函数模型的理论模型,是由 函数在 最大化下导出的。而对数线性需求函数模型和线性需求函数模型则是由 拟合得到的。 7.在线性支出系统需求函数模型 )(∑-+ =j j j i i i i r p V p b r q 中,V 表示总 ,i r 表示第i 种商品的 需求量,i b 表示第i 种商品的边际 份额。 8.在扩展的线性支出系统需求函数模型 )(∑-+ =j j j i i i i r p I p b r q 中,I 表示 ,i r 表示第i 种商 品的 需求量,i b 表示第i 种商品的 消费倾向。 9.在绝对收入假设消费函数模型C Y Y t t t t =+++αββμ012 (t T =12,,,Λ)中,参数a 表示 , 且a 0; t t Y C 10ββ+=,参数b 1<0,表示递减的边际消费倾向。 10.在绝对收入假设消费函数模型 C Y Y t t t t =+++αββμ012 (t T =12,,,Λ)中,参数b 1 0,以反映边际消费倾向 规律。
高级计量经济学之第5章分布滞后与动态模型
第5章 分布滞后与动态模型 §5.1 分布滞后模型 很多经济模型在回归方程中有滞后项,例如,因为修建桥和高速公路需要很多时间,所以公共投资对GDP 的影响有一个滞后期,而且这个影响可能会持续数年;研发新产品需要时间,而后把这个新产品投入生产也需要时间;在研究消费行为时,一个工资的变化可能影响好几期的消费。在消费的恒久收入理论中,消费者会用若干期去决定真实可支配收入的变化是暂时的还是永久的。例如,今年额外的咨询费收入明年是否还会继续?同样,真实可支配收入的滞后值会在回归方程中出现,是因为消费者在平滑其消费行为时十分重视他自身的终身收入。一个人的终身收入可以用他过去和现在的收入来推测。换句话说,回归关系可以写为: T t X X X Y t s t s t t t ,,2,1110 =+++++=--εβββα (5.1) 其中,t Y 代表被解释变量Y 在第t 期的观测值,t s X -代表解释变量X 第t s -期的观测值,α为截距项,0β,1β,…,s β是t X 当期和滞后期的系数。方程(5.1)式就是分布滞后模型因为它把收入增长对消费的影响分为s 期。X 的一个单位变化对Y 的短期影响由0β来表示,而X 的一个单位变化对Y 的长期影响由 (s βββ+++ 10)来表示。 假设我们观察从1955年到1995年的t X ,1t X -为相同的变量,但是提前一期的,也就是1954-1994。因为1954年的数据观察不到,我们就从1955年开始观察 1t X -,到1994年结束。这意味着当我们滞后一期时,t X 序列将从1956年开始到 1995年结束。对于实际的应用来说,也就是当我们滞后一期时,我们将从样本中
期末计量经济学公式
序号 公式名 称 计 算 公式 1 真实的回归模型 y t = ?0 + ?1 x t + u t 2 估计的回归模型 y t =+ x t + 3 真实的回归函数 E(y t ) = ?0 + ?1 x t 4 估计的回归函数 = + x t 5 最小二乘估计公式 ()()() ∑∑∑∑∑∑--=---== -=2 22 2 221X n X Y X n Y X X X Y Y X X x y x b X b Y b i i i i i i i i i 6 和的方 差 7 ? ? 的无偏估 计量 = s 2 = 8 和估计 的方差 ? 9 总平方和TSS ? (y t -) 2 10 回归平方和 RSS ? ( - ) 2 11 误差平方和 ESS ? (y t -)2 = ? ( )2 12 可决系数(确 定系数) =RSS/TSS 13 检验?0,?1 是 否为零的t 统计量 14 ?1的置信区间 -t ? (T -2) ??1 ? + t ? (T -2) 15 单个y T +1的点 预测 = + x T +1
16E(y T+1)的区间 预测 17单个y T+1的区 间预测 18样本相关系数 表 ?多元线性回归模型的主要计算公式 序号公式名称计算公式 1 真实的回归模型Y= X ?+ u 2 估计的回归模型Y = X+ 3 真实的回归函数E(Y) = X ? 4 估计的回归函数= X 5 最小二乘估计公式= (X 'X)-1X 'Y 6 回归系数的方差Var() = ? 2(X 'X)-1 7 ? ? 的无偏估计量= s2 ='/ (T - k) 8 回归系数估计的方差() =(X 'X)-1 9 回归平方和SSR = = '- T 10 总平方和SST = Y 'Y - T 11 残差平方和SSE = ' 12 可决系数 13 调整的可决系数 14 F统计量 15 t统计量 C = (1 x T+1 1 x T+1 2… x T+1 k-1 ) 16 点预测公式
计量经济学公式整理.doc
2:随机误差项的性质 (1)误差项代表了未纳入模型变量的影响; (2)即使模型中包括了决定数学分数的所有变量,其内在随机性也不可避免,这是做任何 努力都无法解释的; (3)u 代表了度量误差; (4)“奥卡姆剃刀原则”,即描述应该尽可能简单,只要不遗漏重要的信息。 3:解释回归结果的步骤 (1)看整个模型的显著性,看F 统计量的值; (2)看单个参数的显著性; (3)解释斜率的经济含义; (4)解释R 2。 4:古典线性回归模型的基本假定(同多元线性回归模型的基本假定相同) (1)所有自变量是确定性变量; (2) (3)自变量之间不存在完全多重共线性。 12:样本回归方程,i e 为残差项, i i i e X b b Y ++=21 总体回归方程,i u 为随机误差项 i i i u X B B Y ++=21 5: 样本回归函数: 随机样本回归函数: 总体回归函数: 随机总体回归方程: 观察值可表示为: 6:普通最小二乘法就是要选择参数1b 、2b ,使得参差平方和最小。 ()()() ∑∑∑∑∑∑--=---==-=2 2 2 22 21X n X Y X n Y X X X Y Y X X x y x b X b Y b i i i i i i i i i i i i i i i i i i i i i i i i i u X Y E Y e Y Y u X B B Y X B B X Y E e X b b Y X b b Y +=+=++=+=++=+=)|(?)|(?21212121
7:R 2的计算公式:( R 2度量了回归模型对Y 变异的解释比例) TSS :总离差平方和 ESS :回归平方和 RSS :残差平方和 (1) (2) (3) 8:F 检验 ) 3,2(~) 3(2 )(. ...23322--+= =∑∑∑n F n e x y b x y b f d RSS f d ESS F t t t t t ()1 //1/1/1P ..-------?=n TSS k n RSS k n RSS p k n RSS k ESS k ESS k ESS F f d SS MSS f d 总离差 来自残差来自回归值值自由度平方和方差来源 9:F 与判定系数R2之间的重要关系 当R2=0,F =0,当R2=1,F 值为无穷大 10:校正的判定系数R 2 ( )k n n R R ----=1112 2 11:普通最小二乘估计量的一些重要性质: ∑∑∑====+=0 ?00 21i i i i i Y e X e n e e X b b Y 21ESS RSS TSS TSS ESS R TSS =+ = RSS ESS TSS +=)()1()1(22 k n R k R F ---=
计量经济学分析模型
计量经济学分析模型
摘要 改革开放以来,我国经济呈迅速而稳定的增长趋势,由于分配机制和收入水平的变化,城镇居民生活水平在达到稳定小康之后,消费结构和消费水平都出现了一些新的特点。本文旨在对近几年,我国城镇年人均收入变动对年人均各种消费变动的影响进行实证分析。首先,我们综合了几种关于收入和消费的主要理论观点;本文根据相关的数据统计数据,运用一定的计量经济学的研究方法,进而我们建立了理论模型。然后,收集了相关的数据,利用EVIEWS软件对计量模型进行了参数估计和检验,并加以修正。最后,我们对所得的分析结果和影响消费的一些因素作了经济意义的分析,并相应提出一些政策建议。并找到影响居民消费的主要因素。 关键词:居民消费;城镇居民;回归;Eviews
目录 摘要.................................................................. II 前言. (1) 1 问题的提出 (2) 2 经济理论陈述 (3) 2.1西方经济学中有关理论假说 (3) 2.2有关消费结构对居民消费影响的理论 (4) 3 相关数据收集 (6) 4 计量经济模型的建立 (9) 5 模型的求解和检验 (10) 5.1计量经济的检验 (10) 5.1.1模型的回归分析 (10) 5.1.2拟合优度检验: (11) 5.1.3 F检验 (11) 5.1.4 T检验 (12) 5.2 计量修正模型检验: (12) 5.2.1 Y与的一元回归 (13) 5.2.2拟合优度的检验 (13) 5.2.3 F检验 (14) 5.2.4 T检验: (15) 5.3经济意义的分析: (15) 6 政策建议 (16) 结论 (17) 参考文献 (19)
计量经济学公式
12:样本回归方程, Y b1 b2X 总体回归方程, e为残差项, e U i为随机误差项 X i) U i b1、b2,使得参差平方和最小。 2:随机误差项的性质 (1)误差项代表了未纳入模型变量的影响; (2 )即使模型中包括了决定数学分数的所有变量,其内在随机性也不可避免,这是做任何努力都无法解释的; (3)u代表了度量误差; (4)“奥卡姆剃刀原则”,即描述应该尽可能简单,只要不遗漏重要的信息。 3:解释回归结果的步骤 (1)看整个模型的显著性,看 F统计量的值; (2 )看单个参数的显著性; (3 )解释斜率的经济含义; (4)解释R2。 4:古典线性回归模型的基本假定(同多元线性回归模型的基本假定相同) (1)所有自变量是确定性变量; (2) (3 )自变量之间不存在完全多重共线性。 Y B1B2X j 5 5: 样本回归函数:Y? b1 b2X i 随机样本回归函数:Y i b1b2X i e i 总体回归函数:E(Y| X i) B1 B2X i 随机总体回归方程:Y i B1 B2X i U i 观察值可表示为: Y i Y? e Y i E(Y 6:普通最小二乘法就是要选择参数 b1 Y b2 X
X i y i b2 茶 X X i X Y Y —2 X i X X i Y nXY Xi nX2
e 2(n 3) 7: R2的计算公式:(R2度量了回归模型对 Y 变异的解释比例) TSS:总离差平方和 ESS:回归平方和 RSS:残差平方和 (1)TSS ESS RSS (2) 1 ESS RSS TSS TSS (3) R 2婪 TSS &F 检验 ESSd.f. RSSd.f. (b 2 y t x 2t R y t x 3t ) 2 '2 yt 2t yt ‘ ?F(2,n 3) F R 2(k 1) F 2 (1 R 2) (n k) 当R2 = 0, F = 0,当R2= 1 , F 值为无穷大 10:校正的判定系数 R2 方差来源 平方和 自由度d.f. SS MSS - d f 来自回归 ESS k 1 ESS/k 1 来自残差 RSS n k RSS/ n k 总、离 TSS n 1 F 值 ESS/k 1 RSS/n k 9: F 与判定系数R2之间的重要关系
计量经济学复习大纲
计量经济学复习大纲 第一章绪论 1. 建立计量经济学模型的步骤及其要点? (1)如何正确选择解释变量? (2)如何确定模型的基本形式? (3)区分时间序列数据、横截面数据和虚变量数据。(4)何谓经济意义检验?检验的方法? (5)计量经济学模型成功的三要素及其关系。 2. 结合实际例子理解结构分析方法(弹性、乘数的运用及其模型参数解释)。 第二章一元线性回归模型理论与方法 1. 回归分析与相关分析的联系与区别? 2. 回归分析的主要目的和内容? 3. 总体回归函数PRF的内涵和形式(确定和随机)。 4. 随机干扰项的定义及其内涵? 5. 样本回归函数的形式及其与PRF的关系? 6. 线性回归模型的基本假设(结合现实经济例子给予解释说明)。 7. OLS法的原理及其参数估计量的估计方法(推导过程)、正规方程组的导出。 8. OLS估计量的计算公式(离差形式)及其参数经济意义解释(要求掌握回归函数的求解计算过程)。
9. OLS估计量的性质(要求掌握线性性、无偏性、有效性的涵义及其证明过程,基本推论要牢记且理解) 10. BLUE估计量与高斯-马尔可夫定理? 11. 一元参数估计量的概率分布形式、总体方差的无偏估计公式以及样本参数的标准差计算公式(要求牢记公式并熟练运用于计算)。 12. 拟合优度检验的原理(TSS、ESS和RSS的内涵及其关系)? 13. 变量显著性检验的方法原理(t检验) (1)小概率事件原理(零假设必须是一小概率事件)?(2)t统计量的构造? 14.. 缩小置信区间的方法:同等显著性水平下尽可能减小t检验临界值和样本参数的标准差。 一是增大样本容量;二是提高模型的拟合优度。 15. 本章练习题第2、3、7、8、9(样本参数估计量的性质)、11题要求熟练掌握。 第三章多元线性回归模型理论与方法 1. 理解偏回归系数的概念及其应用解释。 2. 多元线性回归模型的基本假定(标量和矩阵形式)。 3. 理解普通最小二乘估计的正规方程组及其参数估计量计算公式。 4. 理解最小样本容量的概念及其原理。 5. 熟练掌握和应用调整可决系数的计算公式及其与R2的关系
计量经济学考试重点整理
计量经济学考试重点整理 第一章: P1:什么是计量经济学?由哪三组组成? 定义:“用数学方法探讨经济学可以从好几个方面着手,但任何一个方面都不能和计量经济学混为一谈。计量经济学与经济统计学绝非一码事;它也不同于我们所说的一般经济理论,尽管经济理论大部分具有一定的数量特征;计量经济学也不应视为数学应用于经济学的同义语。经验表明,统计学、经济理论和数学这三者对于真正了解现代经济生活的数量关系来说,都是必要的,但本身并非是充分条件。三者结合起来,就是力量,这种结合便构成了计量经济学。” P9:理论模型的设计主要包含三部分工作,即选择变量,确定变量之间的数学关系,拟定模型中待估计参数的数值范围。 P12:常用的样本数据:时间序列,截面,虚变量数据 P13:样本数据的质量(4点) 完整性;准确性;可比性;一致性 P15-16:模型的检验(4个检验) 1、经济意义检验 2、统计检验 拟合优度检验 总体显著性检验 变量显著性检验 3、计量经济学检验 异方差性检验 序列相关性检验 共线性检验 4、模型预测检验 稳定性检验:扩大样本重新估计 预测性能检验:对样本外一点进行实际预测 P16计量经济学模型成功的三要素:理论、方法和数据。 P18-20:计量经济学模型的应用 1、结构分析 经济学中的结构分析是对经济现象中变量之间相互关系的研究。 结构分析所采用的主要方法是弹性分析、乘数分析与比较静力分析。 计量经济学模型的功能是揭示经济现象中变量之间的相互关系,即通过模型得到弹性、乘数等。 2、经济预测 计量经济学模型作为一类经济数学模型,是从用于经济预测,特别是短期预测而发展起来的。 计量经济学模型是以模拟历史、从已经发生的经济活动中找出变化规律为主要技术手段。 对于非稳定发展的经济过程,对于缺乏规范行为理论的经济活动,计量经济学模型预测功能失效。 模型理论方法的发展以适应预测的需要。
计量经济学简答题(经典)
1 ?什么是计量经济学?它与经济学、统计学和数学的关系怎样?答:1、计量经济学是一门运用经济理论和统计技术来分析经济数据的科学和艺术,它以经济理论为指导,以客观事实为依据,运用数学、统计学的方法和计算机技术,研究带有随机影响的经济变量之间的数量关系和规律。2、经济理论、数学和统计学知识是在计量经济学这一领域进行研究的必要前提,这三者中的每一个对于真正理解现代经济生活中的数量关系是必要的,但不充分,只有结合在一起才行。 2计量经济学三个要素是什么? 经济理论、经济数据和统计方法。 3. 计量经济学模型的检验包括哪几个方面?其具体含义是什么? 答:(1)经济意义检验,即根据拟定的符号、大小、关系,对参数估计结果的可靠性进行判断(2)统计检验,由数理统计理论决定。包括:拟合优度检验、总体显着性检验。(3)计量经济学检验,由计量经济学理论决定。包括:异方差性检验、序列相关性检验、多重共线性检验。(4)模型预测检验,由模型应用要求决定。包括:稳定性检验:扩大样本重新估计;预测性能检验:对样本外一点进行实际预测。 4. 计量经济学方法与一般经济数学方法有什么区别? 答:计量经济学揭示经济活动中各因素之间的定量关系,用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各因素之间的理论关系,用确定性的数学方程加以描述。 5. 计量经济学模型研究的经济关系有那两个基本特征? 答:一是随机关系,二是因果关系J - . ' /■ 6. 计量经济学研究的对象和核心内容是什么? 答:计量经济学的研究对象是经济现象,是研究经济现象中的具体数量规律。计量经济学的核心内容包括两个方面:一是方法论,即计量经济学方法或者理论计量经济学。二是应用,即应用计量经济学。 无论是理论计量经济学还是应用计量经济学,都包括理论、方法和数据三种要素。 7. 计量经济学中应用的数据类型怎样?举例解释其中三种数据类型的结构。 答:计量经济模型:WAGE二f(EDU,EXP,GEND,山 1)时间序列数据是按时间周期收集的数据,如年度或季度的国民生产总值。 2)横截面数据是在同一时间点手机的不同个体的数据。如世界各国某年国民生产总值。 3)混合数据是兼有时间序列和横截面成分的数据,女口 1985 —2010世界各国GDP数据。 8. 建立与应用计量经济学模型的主要步骤有哪些? (1)理论模型的设计(2)样本数据的收集(3)模型参数的估计(4)模型的检验 9. 用OLS建立多元线性回归模型,有哪些基本假设? 1、回归模型是线性的,模型设定无误且含有误差项 2、误差项总体均值为零 3、所有解释变量与误差 项都不相关4、误差项互不相关(不存在序列相关性)5、误差项具有同方差6、任何一个解释变量都不是其他解释变量的完全线性函数7、误差项服从正态分布。 10. 随机误差项包含哪些因素影响? 在解释变量中被忽略的因素的影响(影响不显着的因素、未知的影响因素、无法获得数据的因素);变量观测值的观测误差的影响;模型关系的设定误差的影响;其它随机因素的影响。 11. 为什么要计算调整后的可决系数? 在应用过程中发现,如果在模型中增加一个解释变量,?往往增大。这是因为残差平方和往往随着解 释变量的增加而减少,至少不会增加。这就给人一个错觉:要使得模型拟合得好,只要增加解释变量即可。但是,现实情况往往是,由增加解释变量个数引起的的增大与拟合好坏无关,需调整。 =0.89表示被解释变量Y的变异性的89%能用估计的回归方程解释。 12. 叙述多重共线性的概念、后果和补救措施。 概念:如果两个或多于两个解释变量之间出现了相关性,则称模型存在多重共线性。 后果:1、估计量仍然是无偏的2、参数估计量的方差和标准差增大3、置信区间变宽4、t统计量会变 小5、估计量对模型设定的变化及其敏感6、对方程的整体拟合程度几乎没有影响7、回归系数符号
