高中数学立体几何常考证明题汇总(全)

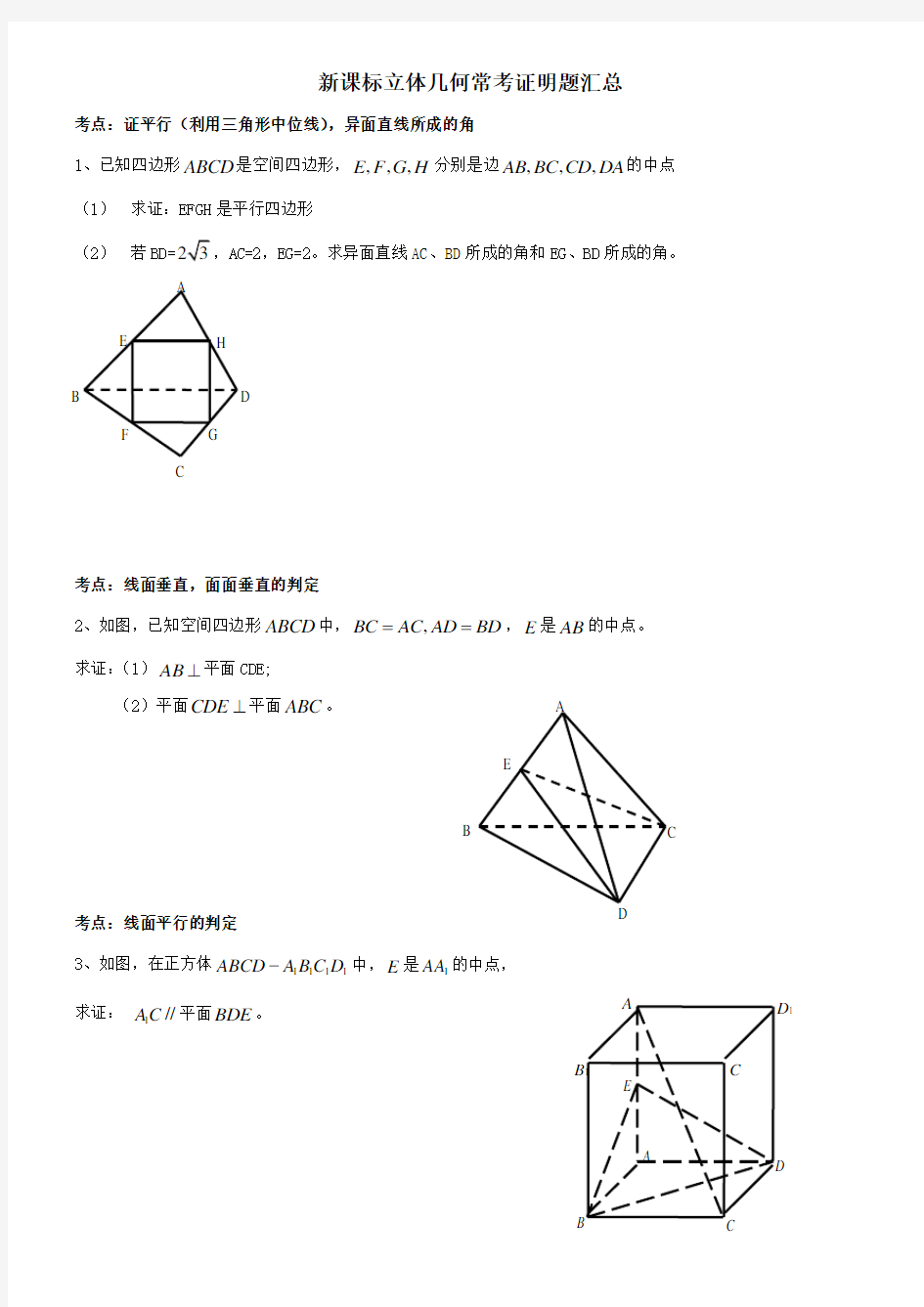
新课标立体几何常考证明题汇总

考点：证平行（利用三角形中位线），异面直线所成的角

1、已知四边形ABCD 是空间四边形，,,,E F G H 分别是边,,,AB BC CD DA 的中点 （1） 求证：EFGH 是平行四边形

（2） 若

BD=AC=2，EG=2。求异面直线AC 、BD 所成的角和EG 、BD 所成的角。

考点：线面垂直，面面垂直的判定

2、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。 求证：（1）⊥AB 平面CDE;

（2）平面CDE ⊥平面ABC 。

考点：线面平行的判定

3、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点， 求证： 1//AC 平面BDE 。

A

E

D 1

C

B 1

D

C

B

A

A

H

G

F

E

D

C

B A

E

D

B

C

考点：线面垂直的判定

4、已知ABC ?中90ACB ∠= ,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．

考点：线面平行的判定（利用平行四边形），线面垂直的判定 5、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.

求证：(１) C 1O ∥面11AB D ；(2)1

AC ⊥面11AB D ．

考点：线面垂直的判定

6、正方体''''ABCD A B C D -中，求证：（1）''AC B D DB ⊥平面；（2）''BD ACB ⊥平面.

考点：线面平行的判定（利用平行四边形）

7、正方体ABCD —A 1B 1C 1D 1中．(1)求证：平面A 1BD ∥平面B 1D 1C ； (2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ．

S

D

C

B

A

D 1O

D

B A

C 1

B 1

A 1

C

A

1

N

M

P

C

B

A

考点：线面垂直的判定,三角形中位线，构造直角三角形

8、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，

且2

EF AC =

， 90BDC ∠= ，求证：BD ⊥平面ACD

考点：三垂线定理

9、如图P 是ABC ?所在平面外一点，,PA PB CB =⊥平面PAB ，M 是PC 的中点，N 是AB 上的点，

3AN NB = （1）求证：MN AB ⊥；（2）当90APB ∠=

，24AB BC ==时，求MN 的长。

考点：线面平行的判定（利用三角形中位线）

10、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点. 求证：平面1D EF ∥平面BDG .

考点：线面平行的判定（利用三角形中位线），面面垂直的判定 11、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. （1）求证：1//AC 平面BDE ； （2）求证：平面1A AC ⊥平面BDE .

考点：线面垂直的判定,构造直角三角形

12、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E

为BC 的中点．

（1）求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角．

考点：线面垂直的判定,构造直角三角形,面面垂直的性质定理，二面角的求法（定义法）

13、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．

（1）若G 为AD 的中点，求证：BG ⊥平面PAD ； （2）求证：AD PB ⊥；

（3）求二面角A BC P --的大小．

考点：线面垂直的判定，运用勾股定理寻求线线垂直

14、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1

AO ⊥平面MBD ．

考点：线面垂直的判定

15、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，

作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．

考点：线面垂直的判定，三垂线定理

16、证明：在正方体ABCD－A1B1C1D1中，A1C⊥平面BC1D

A

C

考点：面面垂直的判定（证二面角是直二面角）

17、如图，过S引三条长度相等但不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC⊥平面BSC．