高三复习专题:不等式证明

高三复习专题:不等式证明
[设计思路]
从近几年的高考试题来看,有关不等式的试题基本上都是一道选择题或填空题和一道解答题,解答题一般是解不等式和证明不等式,纯粹本单元的试题分值逐渐减少,但在一些函数、数列、立体几何、解析几何和实际应用问题的试题中常涉及不等式的知识,在综合题的解题过程中处处分布着不等式的知识、方法和技巧,理科平均约9%,文科约7%。
证明不等式是理科考查的重点,不等式证明题历来难度大,区分度高,综合性强,创新不断,学生平时练习题与试题差距较大,所以教学时一方面要重视对基础知识、基本方法的复习,另一方面更要注重证明方法中蕴含的思想方法、技巧、技能在其他章节知识中的应用,强调知识的综合和知识的内在联系。
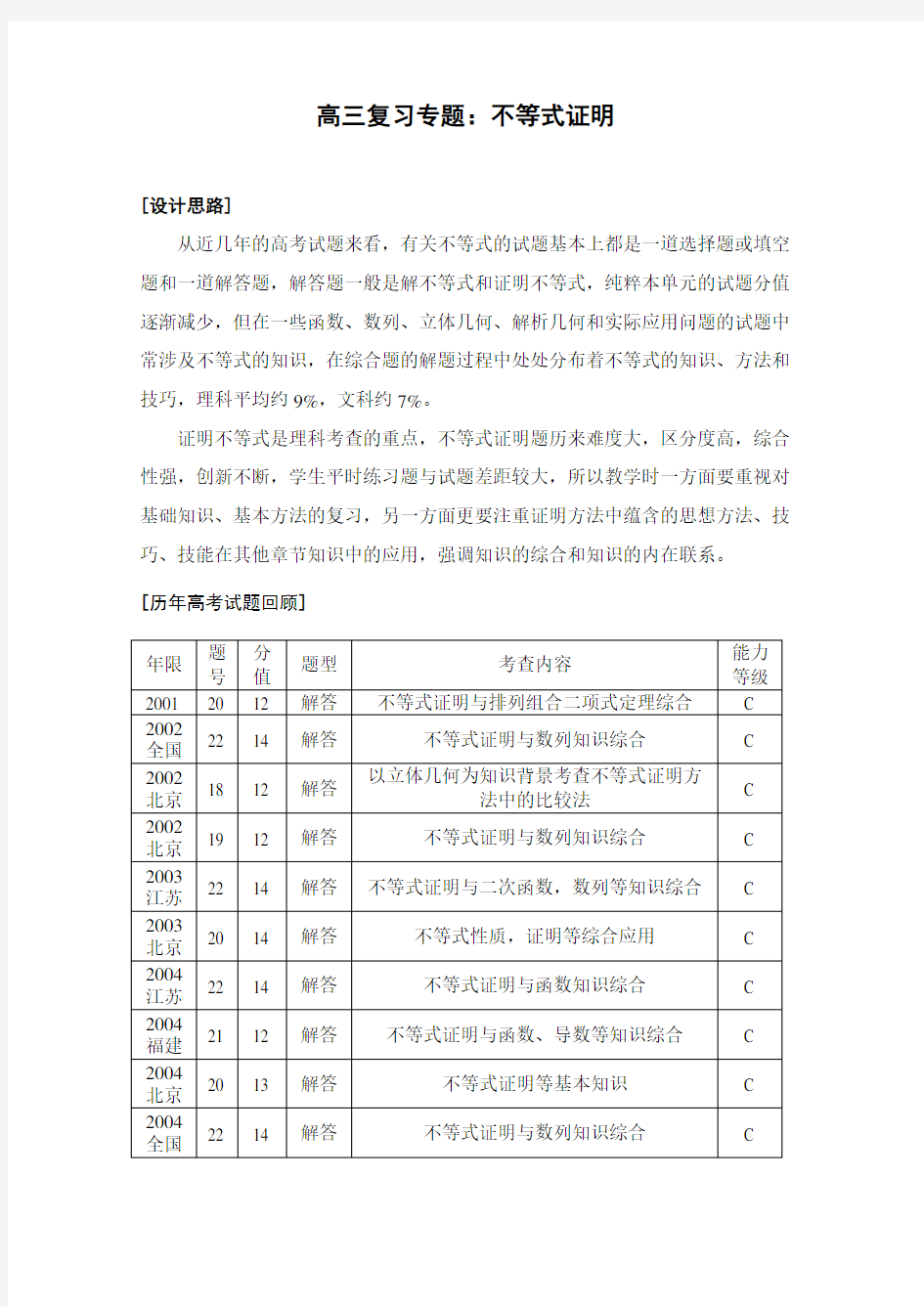
[历年高考试题回顾]
[重点]
不等式证明方法的基本思想方法。
[难点]
不等式证明方法的综合应用。
[课时安排]
第一课时重在复习巩固几种常见的证明方法
第二课时重在培养学生的综合应用能力
[例题设计]
第一课时
揭示主题:这节课我们一起来复习不等式的证明方法, 不等式证明的常用方法有哪些?
不等式证明的方法有比较法,分析法,综合法,放缩法,反证法,换元法等等. 提出问题:
例1 已知在a,b,c∈R+,求证a2b+ab2+a2c+ac2+b2c+bc2≥6abc
学生活动:学生自主思考、分析、回忆、后讨论,最终解决问题。
解法1:比较法
a2b+ab2+a2c+ac2+b2c+bc2-6abc
=a2b-2abc+bc2+ab2-2abc+ac2+a2c-2abc+b2c
=b(a-c) 2+a(b-c) 2+c(a-b) 2
a,b,c∈R+
且(a-c) 2≥0,(b-c) 2≥0,(a-b) 2≥0}→b(a-c) 2+a(b-c) 2+c(a-b) 2≥0
从而a2b+ab2+a2c+ac2+b2c+bc2≥6abc
[知识总结] 比较法包括作差比较法和作商比较法两种,作差比较法是重中之重.
作差比较法的一般步骤________(1)作差;(2)变形(积化和差或配方或通分
等等);(3)定号.
解法2:分析法
要证 a 2b+ab 2a 2c+ac 2+b 2c+bc 2≥6abc
a ,
b ,
c ∈R +,故只要证明6≥+++++a
c
a b b c b a c b c a
而33,33a c b b a c c b a c b a ++≥=++≥= ∴
6≥+++++a
c
a b b c b a c b c a 即证原不等式成立
[知识总结] 分析法是一种执果索因的方法,是从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判断这些条件是否具备的问题.同时要特别注意分析法步骤的书写规范问题. 解法3:综合法
a ,
b ,
c ∈R +
∴ 3≥++b
a
c b c a
∴6≥+++++a
c
a b b c b a c b c a 即证原不等式成立
[知识总结] 综合法是利用某些证明过的不等式和不等式的性质推导出所要证明的不等式成立的方法,它是一种由因导果的方法.它的基础主要是均值不等式. 解法4:
a 2b+a
b 2+a 2c+a
c 2+b 2c+bc 2
=b(a 2+c 2)+a(b 2+c 2)+c(a 2+b 2) ≥2abc+2abc+2abc =6abc=右
∴ 原不等式成立
解法5:
a 2b+a
b 2+a 2c+a
c 2+b 2c+bc 2
=(a 2b+ac 2+b 2c)+(ab 2+a 2c+bc 2) ≥3222322233bc c a ab c b ac b a ??+?? =3abc+3abc=6abc 解法6:
a 2b+a
b 2+a 2c+a
c 2+b 2c+bc 2≥abc bc c b ac c a ab b a 666222222=?????
[知识总结] 均值不等式),(2+∈≥+R b a ab b a 并不仅仅局限于两个数的情形,对于三个数,四个数,…,乃至n 个数都是成立的,即我们可以把均值不等式
),(2+∈≥+R b a ab b a 推广到n 个数的情形.
教师总结:很多题的解法是不唯一的,故解题时大家要多从不同角度、不同层次、不同途径去分析,把所学知识与所答试题迅速建立联系,从而寻找到多种解题思路,也就是我们经常说的“一题多解”“举一反三”。
变题:已知a ,b ,c ∈R +,求证:6≥+++++c
b
a c a
b b
c b a c a
引导学生进行总结归纳 一题多变:
(1)从解法2、解法3均可看出,原不等式等价于不等式 6≥+++++c
b
a c a
b b
c b a c a (2)从解法4可看出,原不等式也等价于不等式 b(a 2+c 2)+(a(b 2+c 2)+c(a 2+b 2)≥6abc
(3)若将不等式的左边进行其他组合,又可得 b 2 (a+c)+a 2 (b+c)+c 2 (a+b)≥6abc
(4)同(3)也可得ab(a+b)+ac(a+c)+(bc)(b+c)≥6abc (5)若给出命题a ,b ,c ∈R +,则(a+b)+(b+c)(c+a)≥8abc
如果把上面不等式左边展开,不难发现它实际也是与原不等式等价的不等式。
(6)在(5)中不等式的基础上,若两边同时除以abc ,则得8)1)(1)(1(≥+++c a
b c a b
(7)对于问题a ,b ,c ∈R +且a+b+c=1,则(1-a)(1-b)(1-c)≥8abc 我们也不难发现它是不等式的一种变形
另外,选择例1的目的一方面是复习不等式证明的常用方法——比较法、分析法、综合法、放缩法等,另一方面是使学生逐渐养成一题多解,并学会解后反思,总结归纳,让学生们在解题过程中提高思维的广阔性、深刻性、灵活性、敏捷性和独创性。
例2 试用多种方法证明:已知a ,b ,c ,d ∈R 求证:))((2222d c b a bd ac ++≤+
教师引导分析:由于观察角度不同,可产生许多种不同的证明方法: 学生活动:积极思考、探究、讨论 归纳如下: 证法1:(分析法)
(1)当ac+bd ≤0时,不等式显然成立
(2)当ac+bd>0,原不等式?(ac+bd)2≤(a 2+b 2)(c 2+d 2) ?2abcd ≤b 2c 2+a 2d 2
?(bc-ad) 2≥0
此不等式显然成立,故原不等式成立. 证法2:(放缩法)
ac+bd ≤|ac+bd|,
∴只需证))((||2222d c b a bd ac ++≤+.(下同证法1)
[知识总结]
常见放缩技巧有:(0)
(1)
1
a b c d a b c d k
k k k k k +++≥++≥++=+如
证法3:(综合法) (a 2+b 2)(c 2+d 2) =a 2c 2+a 2d 2+b 2c 2+b 2d 2
=(a 2c 2+2abcd+b 2d 2)+(b 2c 2-2abcd+a 2d 2) =(ac+bd) 2+(bc-ad) 2≥(ac+bd) 2.
∴bd ac bd ac d c b a +≥+≥++||))((2222.
证法4:(比较法)
(a 2+b 2)(c 2+d 2)-(ac+bd) 2=(bc-ad) 2≥ 0 ∴bd ac bd ac d c b a +≥+≥++||))((2222.
证法5:(换元法) 设a 2+b 2=r 12,c 2+d 2=r 22
则可设a=r 1cos α,b=r 1sin α,c=r 2cos β,d=r 2sin β
∴ac+bd=r 1r 2cos αcos β+r 1r 2sin αsin β
=r 1r 2cos(α-β)≤r 1r 2=))((2222d c b a ++
[知识总结] 换元法这里主要是三角代换,三角代换的题眼点有如
2221,1a b a +=-再如等等
证法6:(构造法)
设向量),(),(d c n b a m
?=
则||||cos ||||n m n m bd ac n m n m
?≤?=+=?>?<
=))((2
222d c b a ++
注意:还可构造函数利用判别式法,还可构造距离公式用解析法证明等等。
[应用练习]:(选自2003年北京卷18题(Ⅲ))
几何体ABCD —A 1B 1C 1D 1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E ,F 两点,上、下底面矩形的长、宽分别为c ,d 与a ,b 且a >c ,b >d ,两底面间的距离为h .. (Ⅰ)在估测该多面体的体积时,经常运用近似公式 V 估=S 中截面·h 来计算.已知它的体积公式是
6h V =(S 上底面+4S 中截面+S 下底面), 试判断V 估与V 的大小关系,并加以证明. (注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截
面.)
参考答案:V 估<V.证明: ∵a >c ,b >d ,∴
h d b c a d b c a ab cd h V V 2
2)224(6+?+-+?+?++=
-估 0))((12
)])((3))((222[12>--=++-++++=
d b c a h
d b c a d b c a ab cd h A
B C
D
E F
A 1 C 1
B 1
D 1 a b c d
∴V 估<V.
小结:不等式的证明方法很多,大家都要熟练掌握,达到灵活运用,通过一题多解、举一反三的训练来提高自己的能力。
第二课时
[高考试题回顾分析] 参看前面的历年高考试题回顾表,总结特征如下:
(一)每年理科卷中都出现;(二)都是解答题形式;(三)考查能力要求都比较高;(四)从内容上来看主要有类(1)本章知识综合(有03北京);(2)与函数知识综合(有03江苏,04江苏,04福建,04辽宁);(3)与数列知识综合(02全国,02北京,03江苏,04全国卷III ,04湖南,04重庆),与立体几何综合(02北京),与排列组合二项式定理综合(01全国卷)
教师总结:可见,涉及不等式证明的问题是高考的一个热门也是一个重点,同时,不等式的证明往往还与其他章节如函数、数列、导数、解析几何等知识综合,尤其是函数和数列。
例1(2002年北京)数列{x n }由下列条件确定:
.),(21,011N n x a
x x a x n
n n ∈+=
>=+ (Ⅰ)证明:对n ≥2,总有a x n ≥; (Ⅱ)证明:对n ≥2,总有1+≥n n x x ;
分析:(Ⅰ)证明:由)(2
1,011n
n n x a x x a x +=>=+及,可归纳证明0>n x
从而有)
()(2
11N n a x a x x a x x n
n n
n n ∈=?≥+=+(均值不等式的应用—综合法),所以,当n ≥2时,a x n ≥成立.
(Ⅱ)证法一:当n ≥2时,因为)(21,01n
n n n x a
x x a x +=
>≥+,所以 021)(212
1≤-?=-+=-+n
n n n n n n x x a x x a x x x ,故当n ≥2时,1+≥n n x x 成立.
(作差比较法)
证法二:当n ≥2时,因为)(2
1,01n
n n n x a
x x a x +
=>≥+,所以
122)(212
22221=+≤+=+=+n
n n n n n n n n
n x x x x a x x x a x x x ,故当n ≥2时,1+≥n n x x 成立. (作商比较法)
点评:此题是以数列为知识背景,把数列与不等式证明综合起来,重点还是考查不等式证明方法中最基本的方法——综合法和比较法。
例2 (2003年北京)设y=f(x)是定义在区间[-1,1]上的函数,且满足条件: (i)f(-1)=f(1)=0;(ii)对任意u ,v ∈[-1,1]都有|f(u)-f(v)|≤|u-v|. (I)证明:对任意的x ∈[-1,1],都有:
x-1≤f(x)≤1-x ;
(II)证明:对任意的u ,v ∈[-1,1],都有:
|f(u)-f(v)|≤1;
(III)在区间[-1,1]上是否存在满足条件的奇函数y=f(x),且使得:
???
???
?
∈-<-∈-<-]
1,21[,|,||)()(|]2
1,0[,|,||)()(|v u v u v f u f v u v u v f u f 当当 若存在,请举一例;若不存在,请说明理由。 解:(I)证明:由题设条件可知,当x ∈[-1,1] |f(x)|=|f(x)-f(1)|≤|x-1|=1-x 即x-1≤f(x)≤1-x
(II)证明:对任意的u ,v ∈[-1,1], 当|u-v|≤1时,有|f(u)-f(v)|≤|u-v|≤1. 当|u-v|>1时,有u ·v<0. 不妨设u<0,则v>0且v-u>1,
所以,|f(u)-f(v))≤|f(u)-f(-1)|+|f(v)-f(1)|≤|u+1|+|v-1|=1+u+1-v=2-(v-u)<1 综上可知,对任意的u ,v ∈[-1,1],都有:
|f(u)-f(v)|≤1.
(III)满足所述条件的函数不存在,理由如下:假设存在函数f(x)满足条件,
则由|f(u)-f(v)|=|u-v|,u ,v ∈[21,1]得|f(21)-f(1)|=| 21-1|=2
1
又f(1)=0,所以|f(21)|=21
(1)
又因为f(x)为奇函数,所以f(0)=0
由条件|f(u)-f(v)|<|u-v|,u,v ∈[0,21]得|f(21)|=|f(21)-f(0)|< 21
(2)
(1)与(2)矛盾,所以假设不成立,即这样的函数不存在;
点评:本题考查函数、不等式等基本知识,考查综合运用数学知识分析问题和解决问题的能力。第(I)小题主要是赋值法的应用,第(II)小题主要是利用绝对值不等式进行放缩,第(III)小题是反证法的应用,其实也可用分类讨论进行证明。
例3 (2004年,江苏)已知函数f(x)(x ∈R)满足下列条件:对任意的实数x 1,x 2都有λ(x 1-x 2)2≤(x 1-x 2)[f(x 1)-f(x 2)]和|f(x 1)-f(x 2)|≤|x 1-x 2|,
其中λ是大于0的常数,设实数a 0,a ,b 满足f(a 0)=0和b=a-λf(a). (1)证明:λ≤1,并且不存在b 0≠a 0,使得f(b 0)=0; (2)证明:(b-a 0)2≤(1-λ2)(a-a 0)2; (3)证明:[f(b)]2≤(1-λ2)[f(a)]2.
分析 (1)利用不等式的传递性及反证法证明; (2)、(3)都是由构造法,结合不等式的传递性证明. 解:(1)任取x 1,x 2∈R ,x 1≠x 2,则由 λ(x 1-x 2)2≤(x 1-x 2)[f(x 1)-f(x 2)],
(1)
和|f(x 1)-f(x 2)|≤|x 1-x 2|,
(2)
可知λ(x 1-x 2)2≤(x 1-x 2)[f(x 1)-f(x 2)]≤|x 1-x 2|·|f(x 1)-f(x 2)|≤|x 1-x 2|2,从而λ≤1. 假设有b 0≠a 0,使得f(b 0)=0,则由(1)式知 0<λ(a 0-b 0)2≤(a 0-b 0)[f(a 0)-f(b 0)]=0,矛盾. 所以不存在b 0≠a 0,使得f(b 0)=0. (2)由b=a-λf(a),
(3)
可知(b-a 0)2=[a-a 0-λf(a)]2=(a-a 0)2-2λ(a-a 0)f(a)+λ2[f(a)]2.
(4)
由f(a 0)=0和(1)式,得
(a-a 0)f(a)=(a-a 0)[f(a)-f(a 0)]≥λ(a-a 0)2.
(5)
由f(a 0)=0和(2)式知,[f(a)]2=[f(a)-f(a 0)]2≤(a-a 0)2. (6)
则将(5)、(6)代入(4)式,得
(b-a 0)2≤(a-a 0)2-2λ2(a-a 0)2+λ2(a-a 0)2=(1-λ2)(a-a 0)2. (3)由(3)式,可知[f(b)]2=[f(b)-f(a)+f(a)]2 =[f(b)-f(a)]2+2f(a)[f(b)-f(a)]+[f(a)]2
≤(b-a)2-2·λ
a
b -[f(b)-f(a)]+[f(a)]2 (用(2)式)
=λ2[f(a)]2-
λ2
(b-a)[f(b)-f(a)]+[f(a)]2 ≤λ2[f(a)]2-λ
2
·λ·(b-a)2+[f(a)]2
(用(1)式)
=λ2[f(a)]2-2λ2 [f(a)]2+[f(a)]2 =(1-λ2) [f(a)]2.
点评:本题是一道给定义题,以函数、不等式等基础知识作为知识背景,将给定条件与已知知识结合,很有一定的难度,是一道考查学生推理论证能力的好题。
追问:这两道题有何异同?
解后总结:解完这两道高考题,我们不难发现它们很相象,都是把不等式与函数知识进行综合,且接合点也类似,比如条件:|f(x 1)-f(x 2)|≤|x 1-x 2|一模一样,结论也都是函数自变点与函数值的一些不等量关系的证明,证明方法、思路也非常像,所以我们可以说这两题是姊妹题,既然这样2003年在北京卷中出现,2004年又在江苏卷出现,可见其重要性,大家要重视。
[应用练习] 对于在区间[m ,n]上有意义的两个函数f(x)与g(x),如果对任
意的x ∈[m ,n]均有|f(x)-g(x)|≤1,则称f(x)与g(x)在[m ,n]上是接近的,否则是非
接近的,设f 1(x)=log a (x-3a)与f 2(x)=log a a x -1
(a>0,a ≠1)是区间[a+2,a+3]上的两
个函数,(1)求a 的取值范围;(2)讨论f 1 (x)与f 2(x)在区间[a+2,a+3]上是否是接近的。
分析:该题信息量较大,先要弄清瞬时定义,理清题意 解:(1)首先
a>0且a ≠1
(1)
又f 1(x)=log a (x-3a)有意义
所以a+2-3a>0 (2) f 2(x)=log a a x -1
有意义
所以a+2-a>0
(3)
由(1)(2)(3) 得0 (2)只须检验|f 1(x)-f 2(x)|≤1在[a+2,a+3]内是否成立. 又因为|f 1(x)-f 2(x)|=|log a (x-3a)(x-a)|=|log a (x 2-4ax+3a 2)| 令|log a (x 2-4ax+3a 2)|≤1 则-1≤log a (x 2-4ax+3a 2)≤1 (*) 设g(x)=x 2-4ax+3a 2,h(x)=log a g(x) 抛物线g(x)开口向上对称轴为x=2a ,且a ∈(0,1) 所以区间[a+2,a+3]在对称轴右侧,故g(x)为[a+2,a+3]上的增函数 从而h(x)是[a+2,a+3]上的减函数 所以[h(x)]max =log a (4-4a) [h(x)]min =h(a+3)=log a (9-6a) 于是(*)式成立的充要条件是 4044log (44)151log (96)1960a a a a a a a a a a ? <≤-≥??-≤??? ????? -≥--≤???<≤??? 所以a ∈(0,12 57 9-] 所以当a ∈(0, 1257 9-]时,f 1(x)与f 2(x)在[a+2,a+3]上是接近的 当a ∈( 12 57 9-,1)时,f 1(x)与f 2(x)在[a+2,a+3]上是非接近的。 [思维能力训练部分] 一、选择题: 1、已知x,y ∈R ,M=x 2+y 2+1,N=x+y+xy ,则M 与N 的大小关系是( ) A 、M ≥N B 、M ≤N C 、M=N D 、不能确定 2、若a (1) b a 11> (2) | |1||1b a > (3) a b a 1 1>-、 (4)22)1 ()1(a b a a +>+ (5)22)1 ()1(a b b a +>+ A 、1 B 、2 C 、3 D 、4 3、在?ABC 中三边长为a ,b ,c ,若c b a 1 ,1,1成等差数列,则b 所对的角( ) A 、是锐角 B 、是直角 C 、是钝角 D 、不能确定 4、已知lg x ·lg y -lg(xy)+1>0且lg(xy)>2那么( ) A 、0 B 、x>10,0 C 、x>10,y>10 D 、0 5、若不等式|x-1| B 、a ≥3 C 、a ≤1 D 、a ≤3 6、若x>0,y>0,且y x a y x +≤+恒成立,则a 的最小值是( ) A 、22 B 、2 C 、2 D 、1 二、填空题: 7、已知点(x 0,y 0)在直线ax+by=0,(a ,b 为常数)上,则2020)()(b y a x -+-的最小值为 。 8、设a ,b ,c ∈R ,且a+b+c=1,则131313+++++c b a 的最大值是_____。 三、解答题: 9、已知f(x)=x 2-x+c 的定义域为[0,1],x 1∈[0,1],x 2∈[0,1],且x 1≠x 2。 (1)证明:|f(x 2)-f(x 1)|<|x 2-x 1|. (2)证明:|f(x 2)-f(x 1)|<21 (南京师大《高中数学复习与练习》下册) 10、(2001,全国,理,20)已知i ,m ,n 是正整数,且1 (I)证明:n i A m i 11、已知正项数列{a n }满足a 1=P(0 n n a a a += +11 (I)求数列的通项a n ; (II)求证:11 4323 21<++???+++n a a a a n 参考答案: 一、ACACBC 二、22b a +,32 三、9、证明:(1)由于f(x 2)-f(x 1)=(x 2-x 1)·(x 2+x 1-1) 因为x 1,x 2∈[0,1],且x 1≠x 2,所以0 所以|f(x 2)-f(x 1)|=|x 2-x 1|·|x 1+x 2-1|<|x 2-x 1|·1=|x 2-x 1| (2)因为f(x)=x 2-x+c=(x-21)2+c-4 1 ,且0≤x ≤1 所以c-41≤f(x)≤c ,于是f(x 1)∈[c-41,c],f(x 2)∈[c-4 1 ,c] -f(x 2)∈[-c, 41-c],所以-41≤f(x 1)-f(x 2)≤4 1 所以|f(x 1)-f(x 2)|≤41<21 10、解:(I)对于1 n i n n n n n n A m i m m m m m m A i m m m A i i n i i m i m 1 111) 1()1(+-? ?????-?=+-??????-?=+-??????-=同理 )1,,2,1(-???=->- k m n k n n m 且有 i i i i i n m i i m n n m A A m A A ∴> 即n (II)由二项式定理,有0 (1),(1)n n i i i i n m n m i i m n m c n c ==+=+=∑∑ 由(I)知(1)i i i m n i m n m A A <<≤ n 因此 0 n n i i i i n m i i m n A A ==>∑∑ 又1 1 001 11,,o o n m n m mn m n m n A A A A ==== ()i i n m i n m A ><≤ 所以1 1 n n i i i i n m i i m n A A ==>∑∑ 又, i i i i i i i i i i n i m i n m m m c n n c A A A A == 1o o o o n m m c n c == 所以0 (1)(1)n n i i i i n m n m i i m n m n A A ==>+>+∑∑即 11、解:(1)由已知得a n+1a n =a n -a n+1 1 11)1(1 1,11 111 -+=?-+===- ∴+p n a n p a p a a a n n n n 得 由 (2)证明:011 10>-∴ < p 1 1 1111141313121211)1(1 34123112114321 1 11321<+-=+-+??????+-+-+-=++??????+?+?+?<++??????+++<-+= ?n n n n n n a a a a n p n a n n 灵溪一高 金海鸥 不等式的证明方法 不等式的证明是高中数学的一个难点,证明方法多种多样,近几年高考出现较为形式较为活跃,证明中经常需与函数、数列的知识综合应用,灵活的掌握运用各种方法是学好这部分知识的一个前提,下面我们将证明中常见的几种方法作一列举。 注意ab b a 22 2 ≥+的变式应用。常用2 222b a b a +≥ + (其中+ ∈R b a ,)来解决有关根式不等式的问题。 一、比较法 比较法是证明不等式最基本的方法,有做差比较和作商比较两种基本途径。 1、已知a,b,c 均为正数,求证: a c c b b a c b a ++ +++≥++1 11212121 证明:∵a,b 均为正数, ∴ 0) (4)(44)()(14141)(2 ≥+=+-+++=+-+-b a ab b a ab ab b a a b a b b a b a b a 同理 0)(41 4141)(2 ≥+= +-+-c b bc c b c b c b ,0) (414141)(2 ≥+=+-+-c a ac a c a c a c 三式相加,可得 01 11212121≥+-+-+-++a c c b b a c b a ∴a c c b b a c b a ++ +++≥++111212121 二、综合法 综合法是依据题设条件与基本不等式的性质等,运用不等式的变换,从已知条件推出所要证明的结论。 2、a 、b 、),0(∞+∈c ,1=++c b a ,求证: 31222≥ ++c b a 证:2 222)(1)(3c b a c b a ++=≥++?∴ 2222)()(3c b a c b a ++-++0 )()()(222222222222≥-+-+-=---++=a c c b b a ca bc ab c b a 3、设a 、b 、c 是互不相等的正数,求证:)(4 4 4 c b a abc c b a ++>++ 证 : ∵ 2 2442b a b a >+ 2 2442c b c b >+ 2 2442a c a c >+∴ 222222444a c c b b a c b a ++>++ ∵ c ab c b b a c b b a 2 2222222222=?>+同理:a bc a c c b 222222>+ b ca b a a c 222222>+ ∴ )(222222c b a abc a c c b b a ++>++ 4、 知a,b,c R ∈,求证: )(22 2 2 2 2 2 c b a a c c b b a ++≥++ ++ + 证明:∵ ) (2 2 2 2 2 2 2 2)(22b a b a b a b a ab ab +≥++≥+∴≥+ 专题04 不等式的证明 知识通关 1.基本不等式 (1)定理1:如果a ,b ∈R ,那么a 2+b 2≥2ab ,当且仅当a =b 时,等号成立. (2)定理2(基本不等式):如果a ,b>0,那么 2 a b ab +≥,当且仅当a=b 时,等号成立. 用语言可以表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数. (3)定理3:如果a ,b ,c 为正数,那么 3 3 a b c abc ++≥a =b =c 时,等号成立. 用语言可以表述为:三个正数的算术平均数不小于(即大于或等于)它们的几何平均数. (4)算术平均—几何平均定理(基本不等式的推广):对于n 个正数a 1,a 2,···,a n ,它们的算术平均数不小于(即大于或等于)它们的几何平均数,即 12123n n n a a a a a a a n ++ +≥??,当且仅当 a 1=a 2=···=a n 时,等号成立. 2.柯西不等式 (1)二维形式的柯西不等式:若a ,b ,c ,d 都是实数,则2 2 2 2 2 ()(+)()a b c d ac bd +≥+,当且仅当 ad=bc 时,等号成立. (2)柯西不等式的向量形式:设α,β是两个向量,则||||||?≥?αβαβ,当且仅当α是零向量或β是零向量或存在实数k 使α=k β时,等号成立. (3)二维形式的三角不等式:设x 1,y 1,x 2,y 2∈R ,22 221212x x y y ++≥211222()()x y x y -+- (4)一般形式的柯西不等式:设1212,, ,,,, ,n n a a a b b b 是实数,则 (22212n a a a ++ +)(222 12n b b b + ++) ≥()2 1122n n a b a b a b +++,当且仅当a i =0或b i =0(i=1,2,···,n )或存在一个数k 使得 a i =k b i (i=1,2,···,n )时,等号成立. 3.不等式证明的方法 (1)比较法 比较法是证明不等式最基本的方法,可分为作差比较法和作商比较法两种. 用微积分理论证明不等式的方法 江苏省扬中高级中学 卞国文 212200 高等数学中所涉及到的不等式,大致可分为两种:函数不等式(含变量)和数值不等式(不含变量).对于前者,一般可直接或稍加变形构造一函数,从而可通过研究所构造函数的性质,进而证明不等式;对于后者,我们也可根据数值不等式的特点,巧妙的构造辅助函数,从而将数值不等式问题转化为函数的问题,研究方法正好与前者相似. 微积分是高等数学中的重要内容,以它为工具能较好的研究函数的形态,有些常规方法难于证明的不等式,若能根据不等式的结构特征,巧妙的构造函数,将不等式问题转化为函数的问题,利用微积分理论研究函数的性质,应用函数的性质证明不等式. 一、用导数定义证明不等式法 1.证明方法根据-导数定义 导数定义:设函数)(x f y =在点0x 的某个邻域内有定义,若极限 x y x x x x x x f x f ??→?→=--lim lim 0 00)()(0 存在,则称函数)(x f 在0x 可导,称这极限为函数)(x f y =在点0x 的导数,记作)(0x f y '=. 2.证明方法: (1)找出0x ,使得)(0x f y '=恰为结论中不等式的一边;(2)利用导数的定义并结合已知条件去研究. 3.例 例1:设函数nx a x a x a x f n sin 2sin sin )(21+++= ,其中n a a a ,,21都为实数, n 为正整数,已知对于一切实数x ,有x x f sin )(≤,试证:1221≤+++n na a a . 分析:问题中的条件与结论不属于同一类型的函数,如果能找出它们之间的关系,无疑能帮助解决此题,可以看出:)0(221f na a a n '=+++ .于是问题可以转化为证明 1)0(≤'f . 证 明 : 因 nx na x a x a x f n cos 2cos 2cos )(21+++=' .则n na a a f +++=' 212)0(. 利 用 导 数 的 定 义 得 : 证明不等式的几种方法 淮安市吴承恩中学 严永飞 223200 摘要:不等式证明是中学数学的重要内容,证明方法多种多样.通常所用的公式法、放缩法只能解决一些较简单的问题,对于较难的问题则束手无策.本文给出了几种特殊方法.如倒数变换法、构建模型法、逆用等比数列求和公式等方法,使解题容易,新颖独特. 关键词:不等式,公式法,构建模型法 前言 证明不等式是中学数学的重要内容之一,内容抽象,难懂,证明方法更是变化多端.通常所用的一些方法如公式法、放缩法只能解决一些较简单的问题,较难的问题则无法解决.本文给出了几种特殊方法.如倒数变换法、构建模型法、逆用等比数列求和公式等方法. 这里所举的几种证明不等式的特殊方法看似巧妙,但如果认真思考,广泛联系,学以致用,一定能使问题得到很好的解决. 1 运用倒数变换证明不等式 这里所说倒数变换是根据具体的题目要求把不等式的部分进行倒数变换,通过化简后使不等式变得简单,更好更快的解决证明问题. 例1 设+∈R z y x ,,,且xyz =1 求证:)(13z y x ++)(13z x y ++)(13y x z +≥2 3 分析 如果先通分再去分母,则不等式将变得很复杂. 令A x =-1,B y =-1 ,C z =-1 ,则+∈R C B A ,,且1=ABC . 欲证不等式可化为 C B A +2+A C B +2+B A C +2≥23(*) 事实上,a 2+22b λ≥ab λ2 (+∈R b a ,,λ), 而当b >0时, a 2/b ≥b a 22λλ-. (*)式左边≥A λ2-2λ(C B +)+ B λ2-2λ(C A +)+C λ2-2λ(A B +) = λ2(λ-1)(C B A ++) ≥λ6(λ-1)3ABC = λ6(λ-1). 令λ=21时,C B A +2+A C B +2+ B A C +2 ≥6×21×(1-21)=23 得证. (这里用到二元平均不等式的变形和三元平均不等式.) 例 2 已知z y x ,,>0,n 为大于1的正整数,且n n x x +1+n n y y +1+n n z z +1=1 求证:n x x +1+n y y +1+n z z +1≤n n 12- 设X为一n维赋范空间,其范数定义为, 1≤p<∞,证明以下命题: 1. ||x||2≤||x||1≤; 2. ||x||p≤||x||1; 3. ||x||q≤||x||p≤,p 从上图可以看出f(x)在x=0时为1,先上升,在x=1达到最大值2p-1,然后下降,但始终≥1。所以有,即,令x=b/a,有a p+b p≤(a+b)p,同理,使用归纳法可 证明:|x1|p+|x2|p+…+|x n|p≤(|x1|+|x2|+…+|x n|)p②(|x1|p+|x2|p+…+|x n|p)1/p≤|x1|+|x2|+…+|x n| 也即||x||p≤||x||1成立。 3. 先证||x||q≤||x||p (p 证明不等式的13种方法 咸阳师范学院基础教育课程研究中心安振平 不等式证明无论在高考、竞赛,还是其它类型的考试里,出现频率都是比较高,证明难度也是比较大的.因此,有必要总结证明不等式的基本方法,为读者提供学习时的参考资料.笔者选题的标准是题目优美、简明,其证明方法基本并兼顾巧妙. 1.排序方法 对问题的里的变量不妨排出大小顺序,有时便于获得不等式的证明. 例1已知,,0a b c ≥,且1a b c ++=,求证: ()22229 1. a b c abc +++≥2.增量方法 在变量之间增设一个增量,通过增量换元的方法,便于问题的变形和处理.例2设,,a b c R + ∈,试证:2222 a b c a b c a b b c c a ++++≥+++.3.齐次化法 利用题设条件,或者其它变形手段,把原不等式转换为齐次不等式. 例3设,,0,1x y z x y z ≥++=,求证: 2222222221.16 x y y z z x x y z +++≤4.切线方法 通过研究函数在特殊点处的切线,利用切线段代替曲线段,来建立局部不等式.例4已知正数,,x y z 满足3x y z ++=,求证: 323235 x y +≤++.. 5.调整方法 局部固定,逐步调整,探究多元最值,便能获得不等式的证明. 例5已知,,a b c 为非负实数,且1a b c ++=,求证:13.4 ab bc ca abc ++-≤ 6.抽屉原理 在桌上有3个苹果,要把这3个苹果放到2个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放2个苹果.这一简单的现象,就是人们所说的“抽屉原理”.巧用抽屉原理,证明某些不等式,能起到比较神奇的效果. 例6(《数学通报》2010年9期1872题)证明:在任意13个实数中,一定能找到两个实数,x y ,使得0.3.10.3x y x ->+7.坐标方法 构造点坐标,应用解析几何的知识和方法证明不等式. 例7已知a b c R ∈、、,a 、b 不全为零,求证: ()()()22 22222 22.a b ac a b bc a b c a b +++++≥+++8.复数方法 构造复数,应用复数模的性质,可以快速证明一些无理不等式. 例8(数学问题1613,2006,5)设,,,0,a b c R λ+ ∈≥求证:9.向量方法 构造向量,把不等式的证明纳入到向量的知识系统当中去. 例9已知正数,,a b c 满足1a b c ++=,求证: 4 ≤. 10.放缩方法 不等式的证明,关键在于恒等变形过程中的有效放大、或者缩小技巧,放和缩应当恰到好处. 例10已知数列{}n a 中,首项132 a = ,且对任意*1,n n N >∈,均有 11n n a a +=++()211332.42 n n n a -+< 不等式证明基本方法 例1 :求证:221a b a b ab ++≥+- 分析:比较法证明不等式是不等式证明的最基本的方法,常用作差法和作商法,此题用作差法较为简便。 证明:221()a b a b ab ++-+- 2221[()(1)(1)]02 a b a b =-+-+-≥ 评注:1.比较法之一(作差法)步骤:作差——变形——判断与0的关系——结论 2.作差后的变形常用方法有因式分解、配方、通分、有理化等,应注意结合式子的形式,适当选 用。 例2:设c b a >>,求证:b a a c c b ab ca bc 2 22222++<++ 分析:从不等式两边形式看,作差后可进行因式分解。 证明:)(222222b a a c c b ab ca bc ++-++ =)()()(a b ab c a ca b c bc -+-+- =)()]()[()(a b ab c b b a ca b c bc -+-+-+- =))()((a c c b b a --- c b a >>Θ,则,0,0,0<->->-a c c b b a ∴0))()((<---a c c b b a 故原不等式成立 评注:三元因式分解因式,可以排列成一个元的降幂形式: =++-++)(222222b a a c c b ab ca bc )())(()(2a b ab b a b a c a b c -++-+-,这样容易发现规律。 例3 :已知,,a b R +∈求证:11()()2()n n n n a b a b a b ++++≤+ 证明:11()()2()n n n n a b a b a b ++++-+ 11n n n n a b ab a b ++=+-- ()()n n a b a b a b =-+- ()()n n a b b a =-- 高等数学中不等式的证明方法 摘要:各种不等式就是各种形式的数量和变量之间的相互比较关系或制约关系,因此, 不等式很自然地成为分析数学与离散数学诸分支学科中极为重要的工具,而且早已成为 专门的研究对象。高等数学中存在大量的不等式证明,本文主要介绍不等式证明的几种 方法,运用四种通法,利用导数研究函数的单调性,极值或最值以及积分中值定理来解 决不等式证明的问题。我们可以通过这些方法解决有关的问题,培养我们的创新精神, 创新思维,使一些较难的题目简单化、方便化。 关键词:高等数学;不等式;极值;单调性;积分中值定理 Abstract: A variety of inequality is the various forms of high-volume and variable comparison between the relationship or constraints. Therefore, Inequality is natural to be a very important tool in Analysis of discrete mathematics and various bran(https://www.360docs.net/doc/2117755224.html, 毕业论文参考网原创论文)ches of mathematics .It has been a special study.Today there are a large number of inequalities in higher mathematics .This paper introduces the following methods about Proof of Inequality ,such as the using of several general methods, researching monotone function by derivative, using extreme or the most value and Integral Mean Value Theorem . We can resolve the problems identified through these methods. It can bring up our innovative spirit and thinking and some difficult topics may be more easy and Convenient , Keyword: Higher Mathematics; Inequality; Extreme value Monotonicity; Integral Mean Value Theorem 文章来自:全刊杂志赏析网(https://www.360docs.net/doc/2117755224.html,) 原文地址: https://www.360docs.net/doc/2117755224.html,/article/16be7113-df3a-4524-a9c3-4ba707524e72.htm 【摘要】不等式证明是高等数学学习中的一个重要内容,通过解答考研数学中出现的 不等式试题,对一些常用的不等式证明方法进行总结。 【关键词】不等式;中值定理;泰勒公式;辅助函数;柯西 施瓦茨;凹凸性 在高等数学的学习过程当中,一个重点和难点就是不等式的证明,大多数学生在遇到不 等式证明问题不知到如何下手,实际上在许多不等式问题都存在一题多解,针对不等式的证 明,以考研试题为例,总结了几种证明不等式的方法,即中值定理法、辅助函数法、泰勒公 使用黎曼和巧妙证明一类和式不等式 摘要:借助黎曼和几何意义得到一类和式不等式的巧妙证明方法:考虑通过图像看出逼近定积分的过程中产生的一系列黎曼和总是大于或小于定积分值,从而建立黎曼和与定积分的不等关系,而和式又常常就是黎曼和,这样便建立了和式和定积分的不等关系,和式不等式便得以简化。 使用黎曼和精确放缩特性做加强命题:通过取出某些项使其不参与定积分的放缩来加强不等式。 关键词:定积分,黎曼和,和式不等式,证明与加强。 对于和式不等式,由于其变幻较为复杂,构造较为精巧,通常不易证明。针对一类有特殊特征的和式不等式,除了使用通常的构造、不等式放缩以外,还可以用黎曼和巧妙证明,从而免去繁杂的构造和放缩,使其证明更加简洁优美。 黎曼和:对一个在闭区间[,]a b 有定义的实值函数f ,f 关于取样分割0,,n x x 、01,,n t t - 的黎曼和 定义为以下和式: 直观地说就是以标记点i t 到x 轴的距离为高,以分割的子区间为长的矩形的面积,它是求积分时在过程的中间形态,当n →+∞,矩形宽0→,则黎曼和就接近于定积分值。 例一(2012天津高考理科数学,20,第(3)问)证明12 2ln(21)21 n i n i =<+-∑( )- *()n N ∈ 分析:本题作为第三小题,原解答使用了第二问的结论,进行构造颇为繁琐,若撇开前两问, 单对此不等式分析,发现12 ln(21)221 n i n i =?<++-∑ 原式,左边是分式的累加,右边是对数函数,联想到1ln ||dx x C x =+?,因而一个简洁的证明就是取2 21 i -的不足黎曼和 证明:1 1 1 2 22 2121n n i dx i i ++=>--∑ ?由于 ……① 112222212121 n n i dx i n x +=∴+<-+-∑ ? 222 ln(21)2121 n i n i n =∴+<+-+∑ 222ln(21)22121 n i n i n =∴++2<++-+∑ 122ln(21)22121n i n i n =+<++-+∑即,舍去 221n + 即证得12ln(21)221 n i n i =<++-∑ 证明不等式的几种常用方法 证明不等式除了教材中介绍的三种常用方法,即比较法、综合法和分析法外,在不等式证明中,不仅要用比较法、综合法和分析法,根据有些不等式的结构,恰当地运用反证法、换元法或放缩法还可以化难为易.下面几种方法在证明不等式时也经常使用. 一、反证法 如果从正面直接证明,有些问题确实相当困难,容易陷入多个元素的重围之中,而难以自拔,此时可考虑用间接法予以证明,反证法就是间接法的一种.这就是最“没办法”的时候往往又“最有办法”,所谓的“正难则反”就是这个道理. 反证法是利用互为逆否的命题具有等价性来进行证明的,在使用反证法时,必须在假设中罗列出各种与原命题相异的结论,缺少任何一种可能,则反证法都是不完全的. 用反证法证题的实质就是从否定结论入手,经过一系列的逻辑推理,导出矛盾,从而说明原结论正确.例如要证明不等式A>B,先假设A≤B,然后根据题设及不等式的性质,推出矛盾,从而否定假设,即A≤B不成立,而肯定A>B成立.对于要证明的结论中含有“至多”、“至少”、“均是”、“不都”、“任何”、“唯一”等特征字眼的不等式,若正面难以找到解题的突破口,可转换视角,用反证法往往立见奇效. 例1 设a、b、c、d均为正数,求证:下列三个不等式:①a+b<c+d; ②(a+b)(c+d)<ab+cd;③(a+b)cd<ab(c+d)中至少有一个不正确. 反证法:假设不等式①、②、③都成立,因为a、b、c、d都是正数,所以 不等式①与不等式②相乘,得:(a +b)2<ab +cd ,④ 由不等式③得(a +b)cd <ab(c +d)≤( 2 b a +)2 ·(c +d), ∵a +b >0,∴4cd <(a +b)(c +d), 综合不等式②,得4cd <ab +cd , ∴3cd <ab ,即cd <31 ab . 由不等式④,得(a +b)2<ab +cd < 34ab ,即a 2+b 2<-3 2 ab ,显然矛盾. ∴不等式①、②、③中至少有一个不正确. 例2 已知a +b +c >0,ab +bc +ca >0,abc >0,求证:a >0,b >0, c >0. 证明:反证法 由abc >0知a ≠0,假设a <0,则bc <0, 又∵a +b +c >0,∴b +c >-a >0,即a(b +c)<0, 从而ab +bc +ca = a(b +c)+bc <0,与已知矛盾. ∴假设不成立,从而a >0, 同理可证b >0,c >0. 例3 若p >0,q >0,p 3+q 3= 2,求证:p +q ≤2. 证明:反证法 假设p +q >2,则(p +q)3>8,即p 3+q 3+3pq (p +q)>8, ∵p 3+q 3= 2,∴pq (p +q)>2. 故pq (p +q)>2 = p 3+q 3= (p +q)( p 2-pq +q 2), 又p >0,q >0 ? p +q >0, ∴pq >p 2-pq +q 2,即(p -q)2 <0,矛盾. 高考数学高三模拟考试试卷压轴题专题六十三不等式的证明 【高频考点解读】 1.了解证明不等式的基本方法:比较法、综合法、分析法、放缩法、数学归纳法. 2.了解柯西不等式、排序不等式以及贝努利不等式. 3.能利用均值不等式求一些特定函数的极值. 【重点知识梳理】 一、比较法证明不等式 (1)求差比较法: 知道a>b ?a -b>0,ab 只要证明a -b>0即可,这种方法称为求差比较法. (2)求商比较法: 由a>b>0?a b >1且a>0,b>0,因此当a>0,b>0时,要证明a>b ,只要证明a b >1即可,这种方法称为求商比较法. 二、综合法与分析法 1.综合法 利用某些已经证明过的不等式和不等式的性质,推导出所要证明的不等式,这种方法叫综合法.即“由因导果”的方法. 2.分析法 证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题,如果能够肯定这些充分条件都已经具备,那么就可以判定原不等式成立,这种方法叫作分析法.即“执果索因”的方法. 3.平均值不等式 定理:如果a ,b ,c 为正数,则a +b +c 3≥3 abc ,当且仅当a =b =c 时,等号成立. 我们称 a + b + c 3 为正数a ,b ,c 的算术平均值,3 abc 为正数a ,b ,c 的几何平均值,定理中的不等式为三个正数的算术—几何平均值不等式,简称为平均值不等式. 4.一般形式的算术—几何平均值不等式 如果a1,a2,…,an 为n 个正数,则a1+a2+…+an n ≥n a1a2…an ,当且仅当a1=a2=…=an 时,等号成立. 【高考考纲突破】 微积分中不等式的证明方法讨论 不等式的证明题经常出现在考研题中,虽然题目各种各样,但方法无非以下几种: 1.利用函数的单调性证明不等式 若在),(b a 上总有0)(>'x f ,则)(x f 在),(b a 单调增加;若在),(b a 上总有0)(<'x f ,则)(x f 在),(b a 单调减少。 注:考研题的难点是,构造恰当的辅助函数,有时需要两次利用函数的单调性证明不等式,有时需要对),(b a 进行分割,分别在小区间上讨论。 例1:证明:当0a b π<<<时, sin 2cos sin 2cos b b b b a a a a ππ++>++. 【分析】 利用“参数变易法”构造辅助函数,再利用函数的单调性证明. 【详解】 令()sin 2cos sin 2cos ,0f x x x x x a a a a a x b πππ=++---<≤≤<, 则 ()sin cos 2sin cos sin f x x x x x x x x ππ'=+-+=-+,且()0f π'=. 又 ()cos sin cos sin 0f x x x x x x x ''=--=-<,(0,s i n 0x x x π<<>时), 故当0a x b π<≤≤<时,()f x '单调减少,即()()0f x f π''>=,则()f x 单调增加,于是()()0f b f a >=,即 sin 2cos sin 2cos b b b b a a a a ππ++>++. 【评注】 证明数值不等式一般需构造辅助函数,辅助函数一般通过移项,使不等式一端为“0”,另一端即为所作辅助函数()f x ,然后求导验证()f x 的增减性,并求出区间端点的函数值(或极限值)。 例2:设2e b a e <<<, 证明)(4ln ln 2 22a b e a b ->-. 【分析】即证a e a b e b 2 222 4ln 4ln ->- 证明: 设x e x x 224ln )(-=?,则 24ln 2)(e x x x -='?, 2ln 12)(x x x -=''?, 所以当x>e 时,,0)(<''x ? 故)(x ?'单调减少,从而当2 e x e <<时, 万方数据 万方数据 几类定积分不等式的证明 作者:王阳, 崔春红 作者单位:河北农业大学中兽医学院,河北定州,073000 刊名: 和田师范专科学校学报 英文刊名:JOURNAL OF HOTAN TEACHERS COLLEGE 年,卷(期):2009,28(3) 被引用次数:0次 参考文献(4条) 1.白银凤微积分及其应用 2001 2.刘连福.许文林高等数学 2007 3.詹瑞清高等数学全真课堂 2003 4.沈燮吕.邵品宗数学分析纵横谈 1991 相似文献(10条) 1.期刊论文杜红敏.Du Hong-min浅谈定积分在不等式证明与因式分解中应用-中国科教创新导刊2009,""(3) 定积分是高中新课程体系中一个新增加的重要内容,很多教师在该部分内容的教学时都与高中其他知识点割裂开未,殊不知,定积分在高中阶段解题中具有广泛的应用,本文以定积分在不等式证明和因式分解中应用为例,探讨定积分在高中解题中的应用. 2.期刊论文陈欢定积分的一个不等式及其应用-福州大学学报(自然科学版)2003,31(6) 线性是定积分最重要的性质之一,在此基础上定性地分析了形如gfn的函数的定积分的随着n的变化趋势,得到一个定理,并利用这个定理重新证明了Holder不等式. 3.期刊论文嵇国平.Ji Guoping定积分在不等式上的应用-常州师范专科学校学报2003,21(2) 不等式的证明是中学教学的一个重要内容,同时也是一个数学难点.由于微积分部分内容逐步渗透到中学数学中,用定积分方法解决不等式证明已成为可能. 4.期刊论文张惠玲.ZHANG Hui-ling定积分中不等式性质的研究-西安航空技术高等专科学校学报2009,27(3) 关于不等式的性质结论中等号成立的问题,在定积分中,进行了研究与探讨,并举例说明了它的应用. 5.期刊论文冯其明含∑nk=1f(k/n)的不等式的一种证法-高等数学研究2003,6(4) 利用定积分的定义及其几何意义可证明一些含∑nk=1f(k)/(n)的不等式. 6.期刊论文侯晓星.HOU Xiao-xing含定积分的不等式证明-泰州职业技术学院学报2005,5(4) 定积分不等式的证明是常见的一种题型.通过对典型例题的分析,利用换元法将被积函数转化为非负函数,或将定积分不等式视为数值不等式,再利用函数的单调性等,论述了含定积分的不等式证明的一般规律及求证方法. 7.期刊论文程仁华.李丽定积分的定义与某些重要不等式的推广应用-景德镇高专学报2004,19(4) 本文通n个正数的调和平均值、几何平均值、算术平均值及k次幂平均值的关系,并利用定积分的定义和连续函数极限的性质推导出函数的上述四种平均值之间的类似关系. 8.期刊论文沈凤英.孙存金.SHEN Feng-ying.SUN Cun-jin Schwarz不等式及旋转体侧面积的计算问题-苏州市职业大学学报2006,17(4) 文章应用Schwarz不等式的知识,给出了旋转体侧面积计算公式的一个新颖的证明,并同时指出用定积分计算旋转体侧面积时应该避免发生的错误. 9.期刊论文林银河关于Minkowski不等式的讨论-丽水师范专科学校学报2003,25(5) 在有关定积分不等式中,Minkowski不等式占有重要地位.将<数学分析>中提到的Minkowski不等式推广到更加一般的情形,从而改进已有的结论. 10.期刊论文刘放不等式(1/n+1+1/n+2+…+1/2n)2《1/2的六种不同证法-宜宾学院学报2003,6(6) 给出了不等式((1)/(n+1)+(1)/(n+2)+…+(1)/(2n))2<(1)/(2)的六种不同证法. 本文链接:https://www.360docs.net/doc/2117755224.html,/Periodical_htsfgdzkxxxb-hwb200903135.aspx 授权使用:中共汕尾市委党校(zgsw),授权号:05ca550e-ea59-4c55-8af2-9da600b00ff2,下载时间:2010年7月 1日 证明不等式的基本方法 导学目标:1.了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法.2.会用比较法、综合法、分析法、反证法、放缩法证明比较简单的不等式. [自主梳理] 1.三个正数的算术—几何平均不等式:如果a ,b ,c>0,那么_________________________,当且仅当a =b =c 时等号成立. 2.基本不等式(基本不等式的推广):对于n 个正数a 1,a 2,…,a n ,它们的算术平均不小于它们的几何平均,即a 1+a 2+…+a n n ≥n a 1·a 2·…·a n ,当且仅当__________________时等号成立. 3.证明不等式的常用五种方法 (1)比较法:比较法是证明不等式最基本的方法,具体有作差比较和作商比较两种,其基本思想是______与0比较大小或______与1比较大小. (2)综合法:从已知条件出发,利用定义、______、______、性质等,经过一系列的推理、论证而得出命题成立,这种证明方法叫综合法.也叫顺推证法或由因导果法. (3)分析法:从要证明的结论出发,逐步寻求使它成立的________条件,直至所需条件为已知条件或一个明显成立的事实(定义 、公理或已证明的定理、性质等),从而得出要证的命题成立为止,这种证明方法叫分析法.也叫逆推证法或执果索因法. (4)反证法 ①反证法的定义 先假设要证的命题不成立,以此为出发点,结合已知条件,应用公理、定义、定理、性质等,进行正确的推理,得到和命题的条件(或已证明的定理、性质、明显成立的事实等)矛盾的结论,以说明假设不正确,从而证明原命题成立,我们把它称为反证法. ②反证法的特点 先假设原命题不成立,再在正确的推理下得出矛盾,这个矛盾可以是与已知条件矛盾,或与假设矛盾,或与定义、公理、定理、事实等矛盾. (5)放缩法 ①定义:证明不等式时,通过把不等式中的某些部分的值________或________,简化不等式,从而达到证明的目的,我们把这种方法称为放缩法. ②思路:分析观察证明式的特点,适当放大或缩小是证题关键. 题型一 用比差法与比商法证明不等式 1.设t =a +2b ,s =a +b 2+1,则s 与t 的大小关系是( A ) ≥t >t ≤t 用微积分理论证明不等式的方法 高等数学中所涉及到的不等式,大致可分为两种:函数不等式(含变量)和数值不等式(不含变量).对于前者,一般可直接或稍加变形构造一函数,从而可通过研究所构造函数的性质,进而证明不等式;对于后者,我们也可根据数值不等式的特点,巧妙的构造辅助函数,从而将数值不等式问题转化为函数的问题,研究方法正好与前者相似. 微积分是高等数学中的重要内容,以它为工具能较好的研究函数的形态,有些常规方法难于证明的不等式,若能根据不等式的结构特征,巧妙的构造函数,将不等式问题转化为函数的问题,利用微积分理论研究函数的性质,应用函数的性质证明不等式. 一、用导数定义证明不等式法 1.证明方法根据-导数定义 导数定义:设函数)(x f y =在点。0x 的某个邻域内有定义,若极限 x y x x x x x x f x f ??→?→=--lim lim 0) ()(0 存在,则称函数)(x f 在0x 可导,称这极限为函数)(x f y =在点0 x 的导数,记作)(0x f y '=. 2.证明方法: (1)找出0x ,使得)(0x f y '=恰为结论中不等式的一边;(2)利用导数的定义并结合已知条件去研究. 3.例 例1:设函数nx a x a x a x f n sin 2sin sin )(21+++= ,其中n a a a ,,21都为实数, n 为正整数,已知对于一切实数x ,有x x f sin )(≤,试证:1221≤+++n na a a . 证 明 : 因 nx na x a x a x f n cos 2cos 2cos )(21+++=' .则 n na a a f +++=' 212)0(. 得:x x f x x f x f x f f x x x ) ()(lim 0)0()()0(lim lim 00 →→→==--= '.由于x x f sin )(≤. 所以1sin )0(lim =≤ '→x x f x .即1221≤+++n na a a . 4.适用范围 用导数定义证明不等式,此方法得适用范围不广,我们应仔细观察问题中的条件与结论之间的关系.有些不等式符合导数的定义,因此可利用导数的定义将其形式转化,以达到化繁为简的目的. 二.用可导函数的单调性证明不等式法 不等式性质的应用 不等式的性质是解不等式、证明不等式的基础和依据。教材中列举了不等式的性质,由这些性质是可以继续推导出其它有关性质。教材中所列举的性质是最基本、最重要的,对此,不仅要掌握性质的内容,还要掌握性质的证明方法,理解掌握性质成立的条件,把握性质之间的关联。只有理解好,才能牢固记忆及正确运用。 1.不等式性质成立的条件 运用不等式的基本性质解答不等式问题,要注意不等式成立的条件,否则将会出现一些错误。对表达不等式性质的各不等式,要注意“箭头”是单向的还是双向的,也就是说每条性质是否具有可逆性。 例1:若0< B .a b a 11>- C .||||b a > D .22b a > 解:∵0<->-b a 。 由b a -< -11,b a 11>,∴(A )成立。 由0<< b a ,||||b a >,∴(C )成立。 由0>->-b a ,2 2 )()(b a ->-,2 2b a >,∴(D )成立。 ∵0<->-a b a , )(11b a a --<-,b a a ->11,∴(B )不成立。 故应选B 。 例2:判断下列命题是否正确,并说明理由。 (1)若0<c ,在2 2c b c a >两边同乘以2 c ,不等式方向不变。∴b a >。 (3)错误。b a b a 1 1,成立条件是0>ab 。 (4)错误。b a >,bd ac d c >?>,当a ,b ,c ,d 均为正数时成立。 2.不等式性质在不等式等价问题中的应用 例3:下列不等式中不等价的是( ) (1)2232 >-+x x 与0432 >-+x x (2)13 8112++ >++ x x x 与82>x (3)35 7354-+>-+x x x 与74>x (4) 023 >-+x x 与0)2)(3(>-+x x A .(2) B .(3) C .(4) D .(2)(3) 解:(1)0432232 2 >-+?>-+x x x x 。 (2)482>?>x x ,44,11 3 8112>?>-≠?++>++ x x x x x x 。 定积分证明题方法总结六篇 定积分是历年数学的考查重点,其中定积分的证明是考查难点,同学们经常会感觉无从下手,小编特意为大家总结了定积分的计算方法,希望对同学们有帮助。 篇一:定积分计算方法总结一、不定积分计算方法 1. 凑微分法 2. 裂项法 3. 变量代换法 1) 三角代换 2) 根幂代换 3) 倒代换 4. 配方后积分 5. 有理化 6. 和差化积法 7. 分部积分法(反、对、幂、指、三) 8. 降幂法 二、定积分的计算方法 1. 利用函数奇偶性 2. 利用函数周期性 3. 参考不定积分计算方法 三、定积分与极限 1. 积和式极限 2. 利用积分中值定理或微分中值定理求极限 3. 洛必达法则 4. 等价无穷小 四、定积分的估值及其不等式的应用 1. 不计算积分,比较积分值的大小 1) 比较定理:若在同一区间[a,b]上,总有 f(x)>=g(x),则 >= ()dx 2) 利用被积函数所满足的不等式比较之 a) b) 当0 2. 估计具体函数定积分的值 积分估值定理:设f(x)在[a,b]上连续,且其最大值为M,最小值为m则 M(b-a) 3. 具体函数的定积分不等式证法 1) 积分估值定理 2) 放缩法 3) 柯西积分不等式 ≤ % 4. 抽象函数的定积分不等式的证法 1) 拉格朗日中值定理和导数的有界性 2) 积分中值定理 3) 常数变易法 4) 利用泰勒公式展开法 五、变限积分的导数方法 篇二:定积分知识点总结 1、经验总结 (1) 定积分的定义:分割—近似代替—求和—取极限 (2)定积分几何意义: ①f(x)dx(f(x)0)表示y=f(x)与x轴,x=a,x=b所围成曲边梯形的面积 ab ②f(x)dx(f(x)0)表示y=f(x)与x轴,x=a,x=b所围成曲边梯形的面积的相a 反数 (3)定积分的基本性质: ①kf(x)dx=kf(x)dx aabb ②[f1(x)f2(x)]dx=f1(x)dxf2(x)dx aaa ③f(x)dx=f(x)dx+f(x)dx aac (4)求定积分的方法:baf(x)dx=limf(i)xi ni=1nbbbbbcb ①定义法:分割—近似代替—求和—取极限②利用定积分几何意义 ’③微积分基本公式f(x)F(b)-F(a),其中F(x)=f(x) ba 篇三:定积分计算方法总结 1、原函数存在定理 ●定理如果函数f(x)在区间I上连续,那么在区间I上高中不等式的证明方法
备战2019高考数学选择题专题04不等式的证明理
微积分证明不等式方法
证明不等式的几种方法
几个范数不等式的证明
|≤||x||2||y||2,令x=( |x1|, |x2|,..., |x n|),y=(1,1, (1) 可得(|x1|+|x2|+…+|x n|)≤(|x1|+| x2|+…+|x n|)1/2n1/2 ||x||1≤成立。 根据Jensen不等式,令α=2,β=1可以证明。 2. 令f(x)= p=1,f(x)=1,所以只考虑p>1的情况
证明不等式的种方法
高中数学基本不等式证明
高等数学中不等式的证明方法
使用定积分巧妙证明一类和式不等式
证明不等式的几种常用方法
高考数学高三模拟考试试卷压轴题专题六十三不等式的证明
高等数学不等式的证明试题及答案
几类定积分不等式的证明
不等式证明的常用基本方法
用微积分理论证明不等式的方法
不等式的证明方法习题精选精讲
定积分证明题方法总结六
