上海大学数值方法报告

2013-2014学年冬季学期

数值方法实验报告

组别第X组

学号1212XXX

姓名XXXX

指导老师XXXX

完成日期201X.XXX

实验一

一、题目

P31

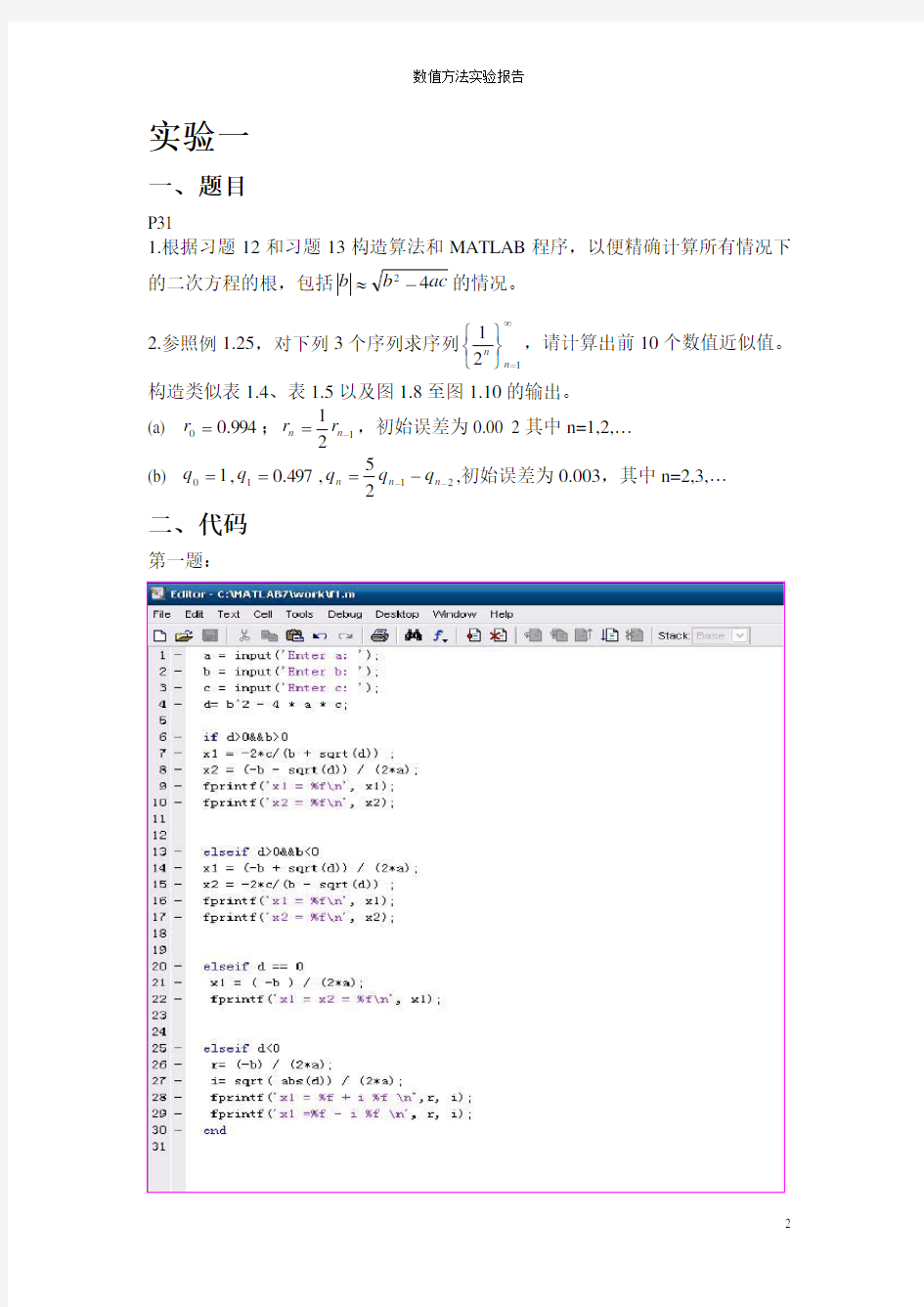
1.根据习题12和习题13构造算法和MATLAB 程序，以便精确计算所有情况下的二次方程的根，包括ac b b 42-≈的情况。

2.参照例1.25，对下列3个序列求序列∞

=???

???1

21n n ，请计算出前10个数值近似值。

构造类似表1.4、表1.5以及图1.8至图1.10的输出。

(a) 994.00=r ；12

1

-=n n r r ，初始误差为0.00 2其中n=1,2,…

(b) 10=q ,497.01=q ,212

5

---=n n n q q q ,初始误差为0.003，其中n=2,3,…

二、代码

第一题：

第二题：

三、结果1、

2、

四、总结

本次作业的目的在于熟悉我们对Matlab基本的操作。第一题是对if…else…

的应用。第二题是画图和格式输出。

实验二

一、题目

P40

1. 使用程序

2.1求解下面每个函数的不动点（尽可能多）近似值，答案精确到小数点后12位。同时，构造每个函数和直线y=x 来显示所有不动点。 （a ） 223)(235+--=x x x x g

（b ） ))cos(sin()(x x g = （c ） )15.0()(2+-=x in x x g （d ）

)cos()(x x x x g -=

P49

3. 修改程序2.2和程序2.3，使得输出分别类似于表2.1和表2.2的矩阵（即矩阵的第一行应当为[0 0a 0c 0b )(0c f ] ）

二、代码

第一题：此题包含了文件fixpt.m 、plotfixpt.m 、sqrtm.m 、main1.m fixpt.m

plotfixpt.m

sqrtm.m

main1.m

function main

figure(1)

hold off

grid on

axis([-2 2.5 -2 2.5]);

axis square

hold on

g=inline('x.^5-3*x.^3-2*x.^2+2');

x=[-2:0.01:2.5];

plot(x,g(x),'r');

plot(x,x,'g');

f1=inline('sqrtm(3*x.^3+2*x.^2+x-2,5)');

plot(x,f1(x),'b');

f2=inline('sqrtm((x.^5-2*x.^2-x+2)/3,3)');

plot(x,f2(x),'c');

f3=inline('sqrt((x.^5-3*x.^3-x+2)./2)');

plot(x,f3(x),'m');

text(-0.9,-0.9,'y=x');

text(-0.4,2.1,'g(x)=x^5-3x^3-2*x^2+2');

text(-1.3,-1.6,'f1(x)=(3x^3+2x^2+x-2)^0^/^5');

text(-0.9,0.3,'f2(x)=((x^5-2x^2-x+2)/3)^1^/^3');

text(-1,1.6,'f3(x)=((x^5-3x^3-x+2)/2)^1^/^2');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% figure(2)

hold off

grid on

axis([-2 2.5 -2 2.5]);

axis square

hold on

[k,p,err,P]=plotfixpt(f1,0.9,0.00001,100,'k');

[k,p,err,P]=plotfixpt(f1,0.6,0.00001,100,'k');

plot(x,g(x),'r');

plot(x,x,'g');

plot(x,f1(x),'b');

text(-0.9,-0.9,'y=x');

text(-0.4,2.1,'g(x)=x^5-3x^3-2*x^2+2');

text(-1.3,-1.6,'f1(x)=(3x^3+2x^2+x-2)^0^/^5');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% figure(3)

hold off

grid on

axis([-2 2.5 -2 2.5]);

axis square

hold on

[k,p,err,P]=plotfixpt(f2,-1,0.00001,100,'k');

plot(x,g(x),'r');

plot(x,x,'g');

plot(x,f2(x),'c');

text(-0.9,-0.9,'y=x');

text(-0.4,2.1,'g(x)=x^5-3x^3-2*x^2+2');

text(-0.9,0.3,'f2(x)=((x^5-2x^2-x+2)/3)^1^/^3');

main2

function main

figure(1)

hold off

grid on

axis([0 2 0 2]);

axis square

hold on

g=inline('cos(sin(x))');

x=[0:0.01:2];

plot(x,g(x),'r');

plot(x,x,'g');

[k,p,err,P]=plotfixpt(g,1.5,0.00001,100,'k');

第二题

function main

g=inline('x.*sin(x)-1');

[c,err,a,b,yc]=bisect(g,0,2,0.0000001);

fprintf(' x sin(x)-1=0\n');

fprintf('--------------------------------------------------------------------------------\n');

fprintf(' k | ak | ck | bk | f(ck) \n');

fprintf('---|------------------|------------------|-------------------|-------------------\n');

maxk=length(yc);

for k=1:maxk

fprintf('%2d | %13.8f | %13.8f | %13.8f | %13.8f

\n',k-1,a(k),c(k),b(k),yc(k));

end

fprintf('---|------------------|------------------|-------------------|-------------------\n');

%

g=inline('x.*sin(x)-1');

[c,err,a,b,yc]=regula(g,0,2,0.0000001,0.0000001,30);

fprintf(' x sin(x)-1=0\n');

fprintf('--------------------------------------------------------------------------------\n');

fprintf(' k | ak | ck | bk | f(ck) \n');

fprintf('---|------------------|------------------|-------------------|-------------------\n'); maxk=length(yc);

for k=1:maxk

fprintf('%2d | %13.8f | %13.8f | %13.8f | %13.8f

\n',k-1,a(k),c(k),b(k),yc(k));

end

fprintf('---|------------------|------------------|-------------------|-------------------\n');

三、结果

第一题：

第二题：

四、总结

本次实验是解方程。第一题是通过迭代法求不动点。第二题是通过二分法（试值法或试位法）求值。本次实验的难点在于多个函数的调用。

实验三

一、题目

P69 第4题

二、代码

function [p0,err,k,y]=newton(A,p0,delta,epsilon,max1)

for k=1:max1

% p1=p0-feval(f,p0)/feval(df,p0);

p1=(2*p0+A/p0/p0)/3; % 把有导数的迭代公式直接换成求导后的公式err = abs(p1-p0);

relerr = 2*err/(abs(p1)+delta);

p0=p1;

%% y= feval(f,p0);

y= p0.^3-A;

if (err

break

end

end

function main

p0=2;

delta=0.0001;

epsilon=0.0001;

max1=20;

A=7;

[p0,err,k,y]=newton(A,p0,delta,epsilon,max1);

fprintf('%f的三次根的值=%.5f\n',A,p0);

p0=6;

delta=0.0001;

epsilon=0.0001;

max1=20;

A=200;

[p0,err,k,y]=newton(A,p0,delta,epsilon,max1);

fprintf('%f的三次根的值=%.5f\n',A,p0);

p0=-2;

delta=0.0001;

epsilon=0.0001;

max1=20;

A=-7;

[p0,err,k,y]=newton(A,p0,delta,epsilon,max1); fprintf('%f的三次根的值=%.5f\n',A,p0);

三、结果

7.000000的三次根的值=1.91294

200.000000的三次根的值=5.84804

-7.000000的三次根的值=-1.91294

四、总结

这题应用的是牛顿—拉夫森迭代公式！

实验四

一、题目

1．93页1题。

2．97页1题。

3．108页1题。

二、代码

第一题：

function main

P=[ 0,0,0;

0,0,1;

0,1,0;

0,1,1;

1,0,0;

1,0,1;

1,1,0;

1,1,1];

P=P';

figure(1)

subplot(1,3,1)

DispCube(P);

subplot(1,3,2)

P=Ry(P,pi/6)

DispCube(P);

subplot(1,3,3)

P=Rz(P,pi/4)

DispCube(P);

End

function DispCube(P)

L1=P(:,[1,2,4,3,1,5,6,8,7,5]); L2=P(:,[2,6]);

L3=P(:,[4,8]);

L4=P(:,[3,7]);

hold off

axis square

plot3(L1(1,:),L1(2,:),L1(3,:)); hold on

plot3(L2(1,:),L2(2,:),L2(3,:)); plot3(L3(1,:),L3(2,:),L3(3,:)); plot3(L4(1,:),L4(2,:),L4(3,:));

axis([-1,2,-1,2,-1,2]);

plot3([0,1.5],[0,0],[0,0],'k'); plot3([0,0],[0,1.5],[0,0],'k'); plot3([0,0],[0,0],[0,1.5],'k'); end

function result = Rx(P,a)

cosa=cos(a);

sina=sin(a);

R=[ 1, 0, 0;

0, cosa, -sina;

0, sina, cosa

];

result = R*P;

end

function result = Ry(P,a)

cosa=cos(a);

sina=sin(a);

R=[ cosa, 0, sina;

0, 1, 0;

-sina, 0, cosa

];

result = R*P;

end

function result = Rz(P,a)

cosa=cos(a);

sina=sin(a);

R=[ cosa, -sina, 0;

sina, cosa, 0;

0, 0, 1

];

result = R*P;

end

第二题：

第三题：

三、结果

第一题：

四、总结

本次实验做的是对线性方程组求解。

实验五

一、题目

120页第一题,第四题(C)

129页第二题

二、代码

第一题：function X=lufact(A,B)

[N N]=size(A);

X=zeros(N,1);

Y=zeros(N,1);

C=zeros(1,N);

R=1:N;

for p=1:N-1

[max1,j]=max(abs(A(p:N,p)));

C=A(p,:);

A(p,:)=A(j+p-1,:);

A(j+p-1,:)=C;

d=R(p);

R(p)=R(j+p-1);

R(j+p-1)=d;

if A(p,p)==0

'A was sinfular. No unique solution'

break

end

for k=p+1:N

mult=A(k,p)/A(p,p);

A(k,p)=mult;

A(k,p+1:N)=A(k,p+1:N)-mult*A(p,p+1:N);

end

end

% Solve for Y

Y(1)=B(R(1));

for k=2:N

Y(k)=B(R(k))-A(k,1:k-1)*Y(1:k-1);

end

% Solve for X

X(N)=Y(N)/A(N,N);

for k=N-1:-1:1

X(k)=(Y(k)-A(k,k+1:N)*X(k+1:N))/A(k,k); end

第二题：

三、结果

第一题：

四、总结

这次实验应用带选主元的分解法。

实验六

一、题目

171页第一题.

202页第一题

二、代码

第一题：

function [C,L]=lagran(X,Y)

w=length(X);

n=w-1;

L=zeros(w,w);

%Form the Lagrange coeddicient polynomials

for k=1:n+1

V=1;

for j=1:n+1

if k~=j

V=conv(V,[1,-X(j)])/(X(k)-X(j));

end

end

L(k,:)=V;

end

%Determine the coefficients of the Lagrange interpolating polynomial

C=Y*L;

function main

X=1:6;

Y=[66 66 65 64 63 63];

[C,L]=lagran(X,Y);

fprintf('Lagran多项式的系数矩阵=\n');

disp(L);

fprintf('多项式系数向量=\n');

disp(C);

addpath('..\P160(4.2.2.1)(多项式计算算法)');

D=fliplr(C); % 翻转向量

aver = (integration(D,6,0)-integration(D,1,0))/5; % 计算从1到6的定积分fprintf('估计在这5个小时内的平均温度=%.4f\n',aver);

x=linspace(1,6,60);