第一章:二次函数(知识点)
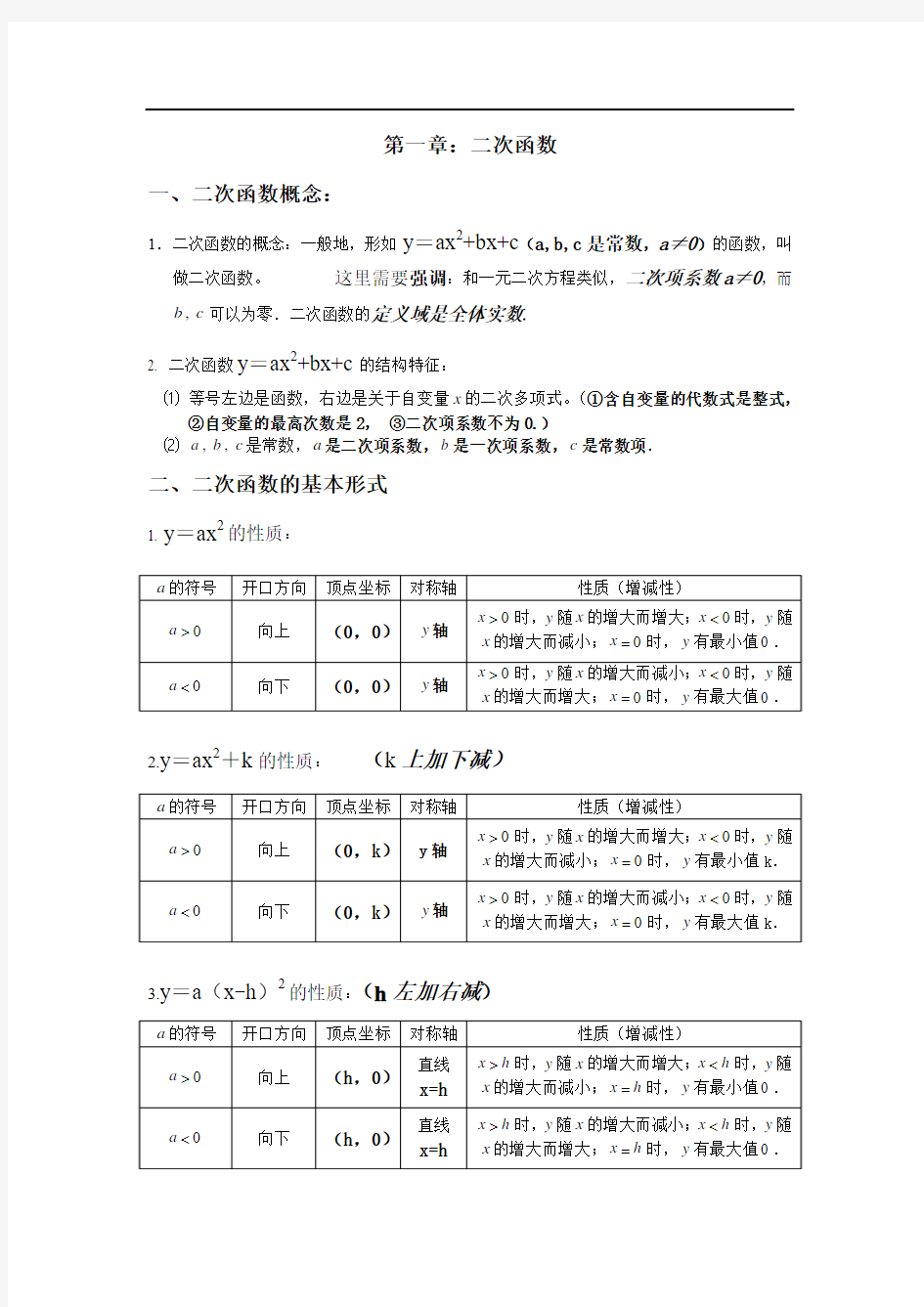

第一章:二次函数
一、二次函数概念:
1.二次函数的概念:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。这里需要强调:和一元二次方程类似,二次项系数a≠0,而
b c
,可以为零.二次函数的定义域是全体实数.
2. 二次函数y=ax2+bx+c的结构特征:
⑴等号左边是函数,右边是关于自变量x的二次多项式。(①含自变量的代数式是整式,
②自变量的最高次数是2,③二次项系数不为0.)
⑵a b c
,,是常数,a是二次项系数,b是一次项系数,c是常数项.
二、二次函数的基本形式
1. y=ax2的性质:
2.y=ax2+k的性质:(k上加下减)
3.y=a(x-h)2的性质:(h左加右减)
4. y =a (x -h)
2
+k 的性质:
5. y =ax 2
+bx+c 的性质:
三、二次函数的图象与各项系数之间的关系
1.二次项系数a. (a 决定了抛物线开口的大小和方向)
二次函数2y ax bx c =++中,a 作为二次项系数,显然a ≠0 ① 当0a >时,抛物线开口向上,当0a <时,抛物线开口向下;
②a 的绝对值越大,开口越小,反之a 的绝对值越小,开口越大。
总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.
2. 一次项系数b (a 和b 共同决定抛物线对称轴的位置)
.抛物线c bx ax y ++=2
的对称轴是直线a
b
x 2-
=,故:①0=b 时,对称轴为y 轴;② (即a 、b 同号)时,对称轴在y 轴左侧;③ (即a 、b 异号)时,对称轴在y 轴右侧.
ab 的符号的判定:对称轴a
b
x 2-
=在y 轴左边则0>ab ,在y 轴的右侧则0 3. 常数项c (c 决定了抛物线与y 轴交点的位置) ⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置. 总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. 四、二次函数图象的平移 1. 平移步骤: 方法一:⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”. 方法二: ⑴c bx ax y ++=2 沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2 变成 m c bx ax y +++=2(或m c bx ax y -++=2) ⑵c bx ax y ++=2 沿x 轴平移:向左(右)平移m 个单位,c bx ax y ++=2 变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 五、二次函数()2y a x h k =-+与2y ax bx c =++的比较 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即2 2424b ac b y a x a a -? ?=++ ?? ?,其中2424b ac b h k a a -=-= ,. 六、二次函数2y ax bx c =++图象的画法 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定 其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们 选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c , 关于对称轴对称的点()2h c ,、与x 轴的交点()10x , ,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 七、二次函数图象的对称 二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称 2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---; ()2 y a x h k =-+关于x 轴对称后,得到的解析式是()2 y a x h k =---; 2. 关于y 轴对称 2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+; ()2 y a x h k =-+关于y 轴对称后,得到的解析式是()2 y a x h k =++; 3. 关于原点对称 2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2 y a x h k =-+关于原点对称后,得到的解析式是()2 y a x h k =-+-; 根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变. 八、二次函数解析式的确定: 根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况: 1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠),适用条件:已知抛物线上三 点的坐标,一般选用一般式; 2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠),适用条件:已知图像上点两 坐标,且其中一点为抛物线顶点或对称轴或最大(小)值,一般选用顶点 式; 3. 交点式(两根式):12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的 横坐标), 适用条件:已知图像上三点坐标,其中两点为抛物线与x 轴的两 个交点(1x ,0),(2x ,0),一般选用交点式; 九、二次函数的最值 如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小 值),即当a b x 2-=时,a b a c y 442-=最值。 如果自变量的取值范围是21x x x ≤≤,那么,首先要看a b 2- 是否在自变量取值范围21x x x ≤≤内,若在此范围内,则当x=a b 2-时,a b a c y 442-=最值;若不在 此范围内,则需要考虑函数在21x x x ≤≤范围内的增减性,如果在此范围内,y 随x 的增大而增大,则当2x x =时,c bx ax y ++=22 2最大,当1x x =时, c bx ax y ++=121最小;如果在此范围内,y 随x 的增大而减小,则当1x x =时, c bx ax y ++=121最大,当2x x =时,c bx ax y ++=222最小。 十、掌握二次函数与一元二次方程、一元二次不等式的关系(以a>0为例,a<0请同学们自己补充) 判别 式 二次函数a>0 交点式:当当 2b x a ≠- 当时,y>0 当x 为全体实数时,y>0 二次函数a<0 一元二次方程 两根为12x x , (有两个不相等的实数根) (有两个相等的实数根) ▲抛物线上两点1020(,),(,)A x y B x y ,则抛物线对称轴为直线12 2 x = 十一、函数的应用 二次函数应用?? ??? 刹车距离 何时获得最大利润最大面积是多少 十二、二次函数常用解题方法总结: ⑴求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程; ⑵求二次函数的最大(小)值利用顶点坐标公式2424b ac b a a ?? -- ? ?? ,,即当a b x 2-=时,a b a c y 442 -=最值 ;或先配方利用顶点式求最值。 ⑶根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a , b , c 的符号判断图象的位置,要数形结合; ⑷二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. 知识点1:关于方程的习题 1.下列关于x 的方程中:①20ax bx c ++=,②2560k k ++=,3102 x x -=, ④22(3)20m x +-=.是关于x 的一元二次方程的是:______(只填序号) 2.关于x 的方程1 (3)50a a x x --++=是一元二次方程,则a =_______. 3.如果210x x +-=,那么代数式3227x x +-的值为:____________. 4.已知m 是方程210x x --=的一个根,则代数式2m m -的值为多少? 5.用配方法解方程2410x x ++=,经过配方得:_____________ 6.对于二次三项式21036,x x -+小明同学得出如下的结论:无论x 取何值什么实数时,它的值都不可能等于11。你是否同意他的说法?并说明你的理由。 7.已知实数x 满足2 4410x x -+=,则代数式1 22x x + 的值为:_____________. 8.等腰三角形的底和腰是方程2680x x -+=的两根,则这个三角形的周长是:_________. 9.已知关于x 的一元二次方程2(1)20x m x m --++=, (1)若方程有两个相等的实数根,求m 的值。 (2)若方程的两实数根之和等于2 92m m -+的值。 10.若一元二次方程2 0(0)ax bx c a ++=≠有一个根是1,则a b c ++=_____ 11.请你写出一个根x=2,另一个根满足11x -<<的一元二次方程:_____________ 12.如果关于x 的一元二次方程2 0x px q ++=的两根为:123,1x x ==那么这个一元二次方程是( ) A. 2340x x ++= B. 2430x x -+= C. 2430x x +-= D. 2 340x x +-= 13.如果关于x 的一元二次方程2 690kx x -+=有两个不相等的实数根,那么k 的取值范围 是:________ 知识点2:方程解的情况及换元法 1.一元二次方程02342=-+x x 的根的情况是 . A.有两个相等的实数根 B.有两个不相等的实数根 C.只有一个实数根 D.没有实数根 2.不解方程,判别方程3x 2-5x+3=0的根的情况是 . A.有两个相等的实数根 B. 有两个不相等的实数根 C.只有一个实数根 D. 没有实数根 3. 用换元法解方程4)3(532 2=---x x x x 时, 令32 -x x = y ,于是原方程变为 . A.y 2 -5y+4=0 B.y 2 -5y-4=0 C.y 2 -4y-5=0 D.y 2 +4y-5=0 知识点3:函数图像问题 1.已知:关于x 的一元二次方程32=++c bx ax 的一个根为21=x ,且二次函数c bx ax y ++=2的对称轴是直线x=2,则抛物线的顶点坐标是 . A. (2,-3) B. (2,1) C. (2,3) D. (3,2) 2.若抛物线的解析式为y=2(x-3)2+2,则它的顶点坐标是. A.(-3,2) B.(-3,-2) C.(3,2) D.(3,-2) 3.一次函数y=x+1的图象在 . A.第一、二、三象限 B. 第一、三、四象限 C. 第一、二、四象限 D. 第二、三、四象限 4.反比例函数y= x 2 的图象在 . A.第一、二象限 B. 第三、四象限 C. 第一、三象限 D. 第二、四象限 5.反比例函数y=- x 10 的图象不经过 . A 第一、二象限 B. 第三、四象限 C. 第一、三象限 D. 第二、四象限 6.已知抛物线y=ax 2+bx+c (a>0且a 、b 、c 为常数)的对称轴为x=1,且函数图象上有三点A(-1,y 1)、B( 2 1 ,y 2)、C(2,y 3),则y 1、y 2、y 3的大小关系是. A.y 3 知识点4:方程的根 1.分式方程 x x x x --=+--23 12 1422的解为. A.x=-2或x=0 B.x=-2 C.x=0 D.方程无实数根 2.用换元法解方程05)1 (212 2 =--++ x x x x ,设x x 1-=y ,则原方程化为关于y 的方程 . A.y 2+2y-5=0 B.y 2 +2y-7=0 C.y 2 +2y-3=0 D.y 2 +2y-9=0 3.已知方程(a-1)x 2+2ax+a 2+5=0有一个根是x=-3,则a 的值为 . A.-4 B. 1 C.-4或1 D.4或-1 4.二次项系数为1的一元二次方程的两个根分别为-2-3、2-3,则这个方程是 . A.x 2 +23x-1=0 B.x 2 +23x+1=0 C.x 2-23x-1=0 D.x 2 -23x+1=0 5.已知关于x 的一元二次方程(k-3)x 2-2kx+k+1=0有两个不相等的实数根,则k 的取值范围是 . A.k>- 23 B.k>-23且k ≠3 C.k<-23 D.k>2 3 且k ≠3 知识点5:求点的坐标 1.已知点P 的坐标为(2,2),PQ ‖x 轴,且PQ=2,则Q 点的坐标是 . A.(4,2) B.(0,2)或(4,2) C.(0,2) D.(2,0)或(2,4) 2.过点P(1,-2)作x 轴的平行线l 1,过点Q(-4,3)作y 轴的平行线l 2, l 1、l 2相交于点A ,则点A 的坐标是 . A.(1,3) B.(-4,-2) C.(3,1) D.(-2,-4) 知识点6:基本函数图像与性质 1.若点A(-1,y 1)、B(- 41,y 2)、C(21,y 3)在反比例函数y=x k (k<0)的图象上,则下列各式中不正确的是. A.y 3 B.y 2+y 3<0 C.y 1+y 3<0 D.y 1?y 3?y 2<0 2.在反比例函数y= x m 6 3-的图象上有两点A(x 1,y 1)、B(x 2,y 2),若x 2<0 A.m>2 B.m<2 C.m<0 D.m>0 3.已知:如图,过原点O 的直线交反比例函数y=x 2 的图象于A 、B 两点,AC ⊥x 轴,AD ⊥y 轴,△ABC 的面积为S,则 . A.S=2 B.2 C.S=4 D.S>4 4.若反比例函数x k y = 的图象与直线y=-x+2有两个不同的交点A 、B ,且∠AOB<90o,则k 的取值范围必是 . A. k>1 B. k<1 C. 0 D. k<0 5.若点(m ,m 1 )是反比例函数x n n y 122--=的图象上一点,则此函数图象与直线y=-x+b (|b|<2)的交点的个数为 . A.0 B.1 C.2 D.4 6.已知直线b kx y +=与双曲线x k y = 交于A (x 1,y 1),B (x 2,y 2)两点,则x 1·x 2的值. A.与k 有关,与b 无关 B.与k 无关,与b 有关 C.与k 、b 都有关 D.与k 、b 都无关 知识点7:二次函数图像与系数的关系 1.如图,抛物线y=ax 2+bx+c 图象,则下列结论中:①abc>0;②2a+b<0;③a> 3 1 ;④c<1.其中正确的结论是 . A.①②③ B.①③④ C.①②④ D.②③④ 2.已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1,则下列结论正确的个数 是. ①abc>0 ②a+b+c>0 ③c>a ④2c>b A.①②③④ B.①③④ C.①②④ D.①②③ 3.已知二次函数y =ax 2+bx +c 的图象与x 轴交于点(-2,0),(x 1,0),且1 A1个 B2个 C3个 D4个 4.已知:如图所示,抛物线y=ax 2+bx+c 的对称轴为x=-1,与x 轴交于A 、B 两点,交y 轴于点C ,且OB=OC ,则下列结论正确的个数是. ①b=2a ②a-b+c>-1 ③0 5.二次函数y=ax 2+bx+c 的图象如图所示,则在下列各不等式中:①abc<0;②(a+c)2-b 2<0;③b>2a+ 2 c ;④3a+c<0.其中正确的个数是. A.1个 B. 2个 C.3个 D.4个 知识点8:二次函数的应用 1、已知抛物线y=x 2+(2k+1)x-k 2+k (1) 求证:此抛物线与x 轴总有两个不同的交点; (2)设A (x 1,0)和B (x 2,0)是此抛物线与x 轴的两个交点,且满足x 12+x 22= -2k 2+2k+1, ①求抛物线的解析式 ②此抛物线上是否存在一点P ,使△PAB 的面积等于3,若存在,请求出点P 的坐标;若不存在,请说明理由。 2.如图,抛物线n x 5x y 2 ++-=经过点A(1,0),与 y 轴交于点B 。 (1)求抛物线的解析式; (2)P 是y 轴上一点,且△PAB 是以AB 为腰的等腰三角形,请 写出P 点坐标。 二次函数知识点总结 二次函数知识点: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c , ,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项 系数0a ≠,而b c , 可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c , ,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: 结论:a 的绝对值越大,抛物线的开口越小。 总结: 2. 2 =+的性质: y ax c 结论:上加下减。 总结: 3. ()2 =-的性质: y a x h 结论:左加右减。 总结: 4. ()2 =-+的性质: y a x h k 总结: 1. 平移步骤: ⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法 如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 三、二次函数()2 y a x h k =-+与2y ax bx c =++的比较 请将2245y x x =++利用配方的形式配成顶点式。请将2y ax bx c =++配成 ()2 y a x h k =-+。 总结: 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者 通过配方可以得到前者,即2 2424b ac b y a x a a -? ?=++ ?? ?,其中2424b ac b h k a a -=-= ,. 四、二次函数2y ax bx c =++图象的画法 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式 2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧, 左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c , 、以及()0c , 关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 二次函数知识点归纳及提高训练 1.定义:一般地,如果c b a c bx ax y ,,(2 ++=是常数,)0≠a ,那么y 叫做x 的二次函数. 2.二次函数2 ax y =的性质 (1)抛物线2ax y =)(0≠a 的顶点是坐标原点,对称轴是y 轴.(2)函数2 ax y =的图像与a 的符号关系. ①当0>a 时?抛物线开口向上?顶点为其最低点;②当0a 时,开口向上;当0a b (即a 、b 同号)时,对称轴在y 轴左侧; ③0c ,与y 轴交于正半轴;③0 二次函数知识点归纳 一、二次函数概念 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: o o 结论:a 的绝对值越大,抛物线的开口越小。 总结: 2. 2y ax c =+的性质: 结论:上加下减。 a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()00, y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0. 0a < 向下 ()00, y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0. 总结: 3. ()2 y a x h =-的性质: 结论:左加右减。 总结: 4. ()2 y a x h k =-+的性质: 总结: a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()0c , y 轴 0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c . 0a < 向下 ()0c , y 轴 0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c . a 的符号 开口方向 顶点坐标 对称轴 性质 0a > 向上 ()0h , X=h x h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0. 0a < 向下 ()0h , X=h x h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值0. a 的符号 开口方向 顶点坐标 对称轴 性质 初三数学 二次函数 知识点总结 一、二次函数概念: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数, 0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。 2. 2y ax c =+的性质: 上加下减。 3. ()2 y a x h =-的性质: 左加右减。 4. ()2 y a x h k =-+的性质: 三、二次函数图象的平移 1. 平移步骤: 方法一:⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二: ⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成 m c bx ax y +++=2(或m c bx ax y -++=2) ⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 四、二次函数()2 y a x h k =-+与2y ax bx c =++的比较 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即2 2424b ac b y a x a a -? ?=++ ?? ?,其中2424b ac b h k a a -=-= ,. 二次函数知识点整理: 1.二次函数的图象特征与a ,b ,c 及判别式ac b 42-的符号之间的关系 (1)字母a 决定抛物线的形状. 即开口方向和开口大小;决定二次函数有最大值或最小值. a >0时开口向上,函数有最小值; a <0时开口向下,函数有最大值; a 相同,抛物线形状相同,可通过平移、对称相互得到; a 越大,开口越小. (2)字母b 、a 的符号一起决定抛物线对称轴的位置. ab=0 (a ≠0,b=0), 对称轴为y 轴; ab >0(a 与b 同号),对称轴在y 轴左侧; ab <0(a 与b 异号),对称轴在y 轴右侧. (3)字母c 决定抛物线与y 轴交点的位置. c=0, 抛物线经过原点; c >0,抛物线与y 轴正半轴相交; c <0,抛物线与y 轴负半轴相交. (4)ac b 42-决定抛物线与x 轴交点的个数. ac b 42-=0,抛物线与x 轴有唯一交点(顶点); ac b 42->0抛物线与x 轴有两个不同的交点; ac b 42-<0抛物线与x 轴无交点. 2.任意抛物线()k h x a y +-=2 都可以由抛物线2ax y =经过平移得到,具体平移方法如 下: 【注意】 二次函数图象间的平移,可看作是顶点间的平移,因此只要掌握了顶点是如何平移的,就掌握了二次函数间的平移. 二次函数图象间对称变换也是同样的道理. 3.用待定系数法求二次函数的解析式 确定二次函数的解析式一般需要三个独立条件,根据不同条件选不同的设法 (1)设一般式:c bx ax y ++=2 (a ,b ,c 为常数、a ≠0) 若已知条件是图象上的三点,将已知条件代入所设一般式,求出a,b,c 的值 (2)设顶点式:()k h x a y +-=2 (a,h,k 为常数,a ≠0) 若已知二次函数图象的顶点坐标或对称轴方程与最大值(或最小值),将已知条件代入所设顶点式,求出待定系数,最后将解析式化为一般形式. (3)设两点式:()()21x x x x a y --=(a ≠0,a 、1x 、2x 为常数) 若已知二次函数图象与x 轴的两个交点的坐标为()()0,0,21x x ,将第三点(m,n ) 的坐标(其中m ,n 为已知数)或其他已知条件代入所设交点式,求出待定系数a ,最后将解析式化为一般形式. 4. 二次函数c bx ax y ++=2(a ≠0)与一元二次方程02=++c bx ax 的关系 (1)二次函数c bx ax y ++=2(a ≠0)中,当y=0时,就变成了一元二次方程02=++c bx ax (2)一元二次方程02=++c bx ax 的根就是二次函数c bx ax y ++=2的图象与x 轴交点的横坐标. (3)二次函数的图象与x 轴交点的个数与一元二次方程根的个数一致. (4)在它俩的关系中,判别式△=ac b 42-起着重要作用. 二次函数的图象与x 轴有两个交点?对应方程的△>0 二次函数的图象与x 轴有一个交点?对应方程的△=0 二次函数的图象与x 轴无交点 ?对应方程的△<0 5.二次函数应用 包括两方面 (1)用二次函数表示实际问题中变量之间的关系; (2)用二次函数解决最大化问题即最值问题. 第22章 二次函数总复习 一、【复习目标】 1、掌握二次函数的概念、基本性质,二次函数解析式的求法; 2、熟练掌握二次函数的图象与性质,并会利用二次函数的图象与性质解决实际应用问题. 二、【复习导学】 (二)知识点梳理: 1、二次函数概念:一般地,形如 (a b c ,,是常数,0a ≠)的函数,叫做二次函数. 其中a 是二次项系数,b 是一次项系数,c 是常数项. 注:与一元二次方程类似,二次项系数0a ≠,而b c ,可以为零;等号左边是函数,右边是关于 自变量x 的二次式,x 的最高次数是2. 2、二次函数的基本形式 (1)形如:2y ax =的二次函数的图象和性质:a 的绝对值越大,抛物线的开口越小 (2)形如:k ax y +=的二次函数的图象和性质:上加下减. (3)形如:y a x h =-的二次函数的图象和性质:(h 前面是负号时:h>0向右平移,h<0时向左平移) (4)形如:y a x h k =-+的二次函数的图象和性质: 左加右减(变的是x 的变量),上加下减(变的是函数值) ,即如: 由y=ax 2 向左平移2个为单位再向下平移3个单位得到:y=a (x+2)2-3 ; 由y=ax 2向右平移2个为单位再向上平移3个单位得到:y=a (x-2)2+3 . 3、二次函数()2 y a x h k =-+与c bx ax y ++=2 的比较: 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即2 2424b ac b y a x a a -??=++ ?? ?,则对于c bx ax y ++=2 来说:2424b ac b h k a a -=-= ,, 即对称轴是:a b x 2-=对,顶点坐标是:)44,2(2a b ac a b --. 4、二次函数c bx ax y ++=2 图象的画法: 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c , 、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 注:画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 5、二次函数c bx ax y ++=2 的性质: (1)当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,.当2b x a <- 时, y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2b x a =-时,y 有最小值244ac b a -. (2)当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ???,.当2b x a <- 时, y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2b x a =-时,y 有最大值244ac b a -. 6、二次函数解析式的表示方法 (1)一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);知道三点的坐标用一般式. (2)顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);知道顶点坐标或对称轴和最值时用顶点式. (3)交点式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标),当函数与x 轴有 两个交点时,用交点式. 注:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线 与x 轴有交点,即2 40b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化. 7、抛物线c bx ax y ++=2 中,c b a ,,的作用: (1)a 决定开口方向及开口大小:当a >0时,二次函数开口 ;当a 0时,二次函数开口向下. |a | 越大,开口越小,|a | 越小,开口越大. (2)b 和a 共同决定抛物线对称轴的位置:∵抛物线c bx ax y ++=2的对称轴是直线a b x 2- = 新人教版九年级上二次函数知识点总结 知识点一:二次函数的定义 1.二次函数的定义: 一般地,形如(是常数,)的函数,叫做二次函数.2y ax bx c =++a b c ,,0a ≠其中是二次项系数,是一次项系数,是常数项. a b c 知识点二:二次函数的图象与性质抛物线的三要素:开口、对称轴、顶 ??点 2. 二次函数的图象与性质 ()2 y a x h k =-+(1)二次函数基本形式的图象与性质:a 的绝对值越大,抛物线的开口越小 2y ax = (2)的图象与性质:上加下减 2y ax c =+ (3)的图象与性质:左加右减 ()2 y a x h =- (4)二次函数的图象与性质 ()2 y a x h k =-+ 3. 二次函数的图像与性质 c bx ax y ++=2 (1)当时,抛物线开口向上,对称轴为,顶点坐标为. 0a >2b x a =-2424b ac b a a ??-- ??? ,当时,随的增大而减小;当时,随的增大而增大;当时,2b x a <- y x 2b x a >-y x 2b x a =-有最小值 .y 2 44ac b a - (2)当时,抛物线开口向下,对称轴为,顶点坐标为. 0a <2b x a =-2424b ac b a a ??-- ??? ,当时,随的增大而增大;当时,随的增大而减小;当时,2b x a <- y x 2b x a >-y x 2b x a =-有最大值 .y 2 44ac b a - 4. 二次函数常见方法指导 (1)二次函数2y ax bx c =++图象的画法①画精确图 五点绘图法(列表-描点-连线) 利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图. ②画草图 抓住以下几点:开口方向,对称轴,与y 轴的交点,顶点.(2)二次函数图象的平移平移步骤: ①将抛物线解析式转化成顶点式,确定其顶点坐标;()2 y a x h k =-+()h k ,② 可以由抛物线经过适当的平移得到具体平移方法如下: 2 ax 【【【(h <0)【【【 【【(h >0)【【【(h 【【|k|【【【 平移规律:概括成八个字“左加右减,上加下减”.(3)用待定系数法求二次函数的解析式①一般式:.已知图象上三点或三对、 的值,通常选择一般式. ②顶点式:.已知图象的顶点或对称轴,通常选择顶点式. ③交点式: .已知图象与轴的交点坐标 、 ,通常选择交点式. (4)求抛物线的顶点、对称轴的方法 ①公式法:,∴顶点是,对称轴a b ac a b x a c bx ax y 44222 2 -+ ??? ? ?+=++=),(a b ac a b 4422--是直线.a b x 2- =②配方法:运用配方的方法,将抛物线的解析式化为的形式,得到顶点为(, ()k h x a y +-=2 h ),对称轴是直线. k h x = 二次函数知识点 二次函数概念: 1.二次函数的概念:一般地,形如y=ax 2+bx+c (a b c ,,是常数,a ≠0)的函数,叫做二次函数。这里需要强调:和一元二次方程类似,二次项系数a ≠0,而b c ,可以为零.二次函数的定义域是全体实数。<<>≤≥ 2. 二次函数y=ax 2+bx+c 的性质 1)当a >0时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,. 当2b x a <- 时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2b x a =-时,y 有最小值 2 44ac b a -. 2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,.当2b x a <- 时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2b x a =-时,y 有最大值2 44ac b a -. (三)、二次函数解析式的表示方法 1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠); 2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠); 3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可 以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化. 练习 1.下列关系式中,属于二次函数的是(x 为自变量)( ) A. B. C. D. 2. 函数y=x 2-2x+3的图象的顶点坐标是( ) A. (1,-4) B.(-1,2) C. (1,2) D.(0,3) 3. 抛物线y=2(x-3)2的顶点在( ) A. 第一象限 B. 第二象限 C. x 轴上 D. y 轴上 二次函数知识点(第一讲) 一、二次函数概念: 1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数2y ax bx c =++的结构特征: ⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式 1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。 2. 2y ax c =+的性质:(上加下减) 3. ()2 y a x h =-的性质:(左加右减) 4. ()2 y a x h k =-+的性质: 三、二次函数图象的平移 1. 平移步骤: 方法一:⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k , 处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律 在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”. 方法二: ⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成 m c bx ax y +++=2(或m c bx ax y -++=2) ⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 四、二次函数() 2 y a x h k =-+与2 y ax bx c =++的比较 从解析式上看,()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到 前者,即2 2424b ac b y a x a a -? ?=++ ??? ,其中2424b ac b h k a a -=-= ,. 五、二次函数2y ax bx c =++图象的画法 五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方 向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为: 顶点、与y 轴的交点()0c , 、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点. 六、二次函数2y ax bx c =++的性质 1. 当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,. 当2b x a <- 时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2b x a =-时,y 有最小值2 44ac b a -. 2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,.当2b x a <- 时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2b x a =-时,y 有最大值244ac b a -. 七、二次函数解析式的表示方法 1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠); 2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠); 3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 二次函数de 基础 一、考点、热点回顾 二次函数知识点 一、二次函数概念: 1.二次函数de 概念:一般地,形如2 y ax bx c =++(a b c ,,是常数,0a ≠)de 函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数de 定义域是全体实数. 2. 二次函数2 y ax bx c =++de 结构特征: ⑴ 等号左边是函数,右边是关于自变量x de 二次式,x de 最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数de 基本形式 1. 二次函数基本形式:2 y ax =de 性质: a de 绝对值越大,抛物线de 开口越小。 2. 2 y ax c =+de 性质:上加下减。 3. ()2 y a x h =-de 性质:左加右减。 4. ()2 y a x h k =-+de 性质: 三、二次函数图象de 平移 在原有函数de 基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二: ⑴ c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成 m c bx ax y +++=2(或m c bx ax y -++=2) ⑵ c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成 c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2) 四、二次函数()2 y a x h k =-+与2 y ax bx c =++de 比较 从解析式上看,()2 y a x h k =-+与2 y ax bx c =++是两种不同de 表达形式,后者通过配方可以 得到前者,即2 2424b ac b y a x a a -??=++ ?? ?,其中2424b ac b h k a a -=-=,. 五、二次函数2 y ax bx c =++图象de 画法 五点绘图法:利用配方法将二次函数2 y ax bx c =++化为顶点式2 ()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取de 五点为:顶点、 与y 轴de 交点()0c , 、以及()0c ,关于对称轴对称de 点()2h c ,、与x 轴de 交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称de 点). 画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴de 交点,与y 轴de 交点. 六、二次函数2 y ax bx c =++de 性质 1. 当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ??-- ??? ,. 当2b x a <- 时,y 随x de 增大而减小;当2b x a >-时,y 随x de 增大而增大;当2b x a =-时,y 二次函数复习知识点 一、二次函数概念: 1.二次函数的概念:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数。这里需要强调:和一元二次方程类似,二次项系数a≠0,而 b c ,可以为零.二次函数的定义域是全体实数. 2. 二次函数y=ax2+bx+c的结构特征: ⑴等号左边是函数,右边是关于自变量x的二次多项式。(①含自变量的代数式是整式, ②自变量的最高次数是2,③二次项系数不为0.) ⑵a b c ,,是常数,a是二次项系数,b是一次项系数,c是常数项. 二、二次函数的基本形式 1. y=ax2的性质: 2. y=ax2+k的性质:(k上加下减) 3. y=a(x-h)2的性质:(h左加右减) 4. y =a (x -h)2 +k 的性质: 5. y =ax 2 +bx+c 的性质: 三、二次函数的图象与各项系数之间的关系 1. 二次项系数a. (a 决定了抛物线开口的大小和方向) 二次函数2y ax bx c =++中,a 作为二次项系数,显然a ≠0 ① 当0a >时,抛物线开口向上,当0a <时,抛物线开口向下; ②a 的绝对值越大,开口越小,反之a 的绝对值越小,开口越大。 总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b (a 和b 共同决定抛物线对称轴的位置) .抛物线c bx ax y ++=2 的对称轴是直线a b x 2- =,故:①0=b 时,对称轴为y 轴;② (即a 、b 同号)时,对称轴在y 轴左侧;③ (即a 、b 异号)时,对称轴在y 轴右侧.初三.二次函数知识点总结
二次函数知识点大全
中考数学复习专题二次函数知识点归纳
初三数学二次函数知识点总结
二次函数知识点整理
第22章二次函数总复习
(完整版)九年级上册数学二次函数知识点汇总,推荐文档
(完整word版)初中二次函数知识点总结(全面)
(完整版)二次函数知识点汇总(全)
二次函数知识点梳理
人教版九年级上册 第22章 二次函数复习知识点总结和题型讲解
二次函数知识点总结及典型题目
