第十七章多元函数的微分学

第十七章 多元函数的微分学
§1 可微性
教学目的 掌握多元函数偏导数,可微性与全微分的定义,可微的必要条件. 教学要求
(1) 基本要求:掌握多元函数偏导数,可微性与全微分的定义,熟记可微的必要条件与充分条件.
(2) 较高要求:切平面存在定理的证明.
教学建议
(1)本节的重点是多元函数偏导数,可微性与全微分的定义.
(2) 通过讨论可微的必要条件与充分条件,弄清多元函数连续,存在偏导数与可微这三个分析性质之间的关系.
教学程序
一、 可微性与全微分:
由一元函数可微性引入二元函数可微性.
定义1(可微性) 设函数(,)z f x y =在点000(,)P x y 的某邻域0()U P 内有定义,对于0()U P 中的点00(,)(,)P x y x x y y =+?+?,若函数f 在点0P 处的全增量可表示为 00(,)(,)()z f x x y y f x y A x B y ρ?=+?+?-=?+?+,其中A ,B
是仅与点0P 有关的常数,()ρρ=是较ρ高阶的无穷小量,则称函数f 在点0P 处可微。
全微分:
当,x y ??充分小时
0000(,)(,)()()dz z
f x y f x y A x x B y y ≈?≈+-+-. 例1 考查函数xy y x f =),(在点) , (00y x 处的可微性 .
二 、 偏导数
(一)、偏导数的定义、记法
),(y x f 在点),(00y x 存在偏导数定义为:
000000),(),(lim ),(0x x y x f y x f y x f x x x --=→ 或 x
y x f y x x f y x f x x x ?-?+=→?),(),(lim ),(0000000 000000),(),(lim ),(0
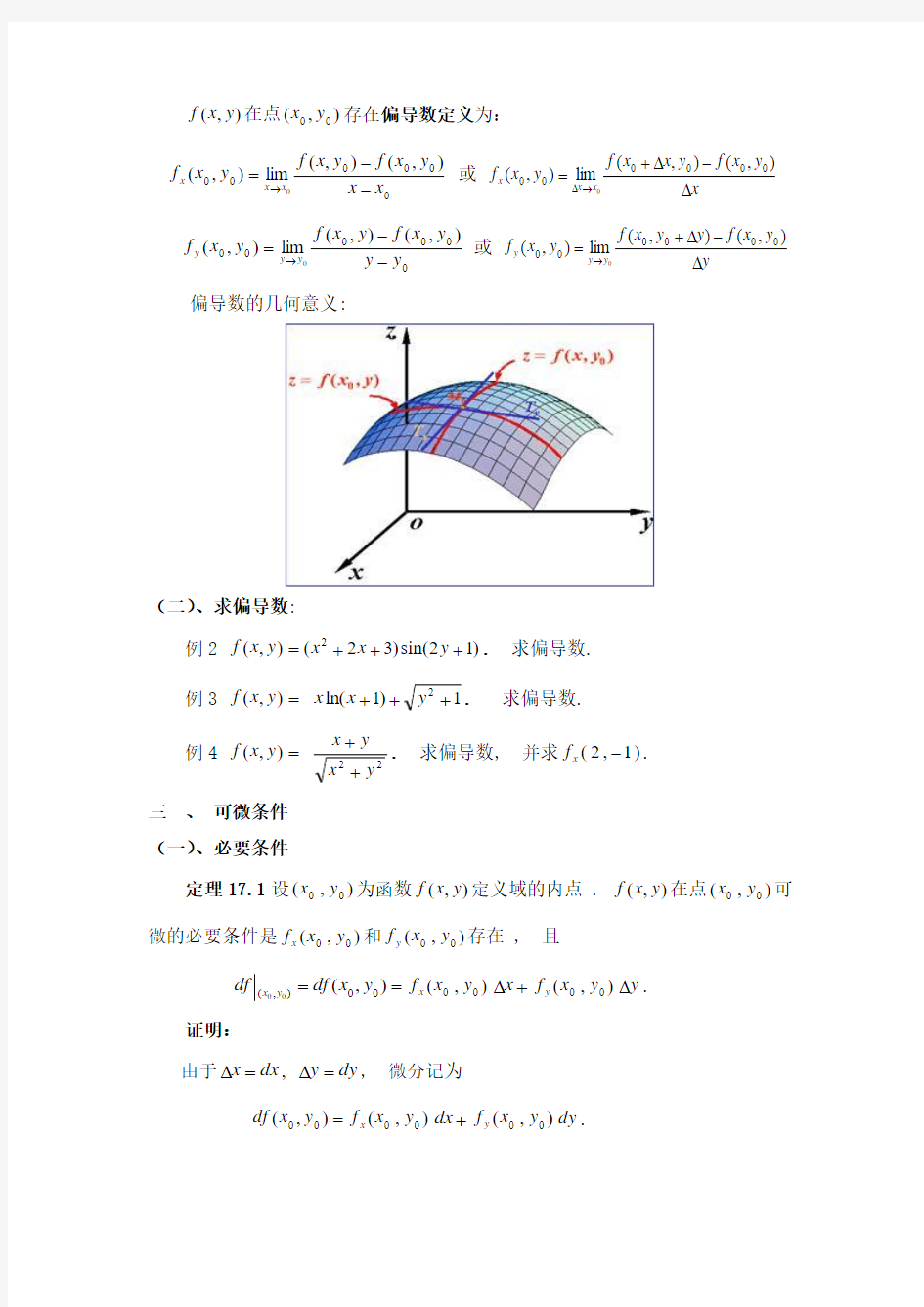
y y y x f y x f y x f y y y --=→ 或 y y x f y y x f y x f y y y ?-?+=→),(),(lim ),(0000000 偏导数的几何意义:
(二)、求偏导数:
例2 ),(y x f =)12sin()32(2+++y x x . 求偏导数.
例3 ),(y x f = 1)1ln(2+++y x x . 求偏导数.
例4 ),(y x f =
22y x y x ++. 求偏导数, 并求) 1 , 2 (-x f . 三 、 可微条件
(一)、必要条件
定理17.1设) , (00y x 为函数),(y x f 定义域的内点 . ),(y x f 在点) , (00y x 可微的必要条件是) , (00y x f x 和) , (00y x f y 存在 , 且 ==),(00),(00y x df df
y x ) , (00y x f x +?x ) , (00y x f y y ?.
证明:
由于dy y dx x =?=? , , 微分记为
=),(00y x df ) , (00y x f x +dx ) , (00y x f y dy .
定理17.1给出了计算可微函数全微分的方法. 但是两个偏导数存在只是可微的必要条件, 而不是充分条件.
例5.考查函数 ?????=+≠++=
0 , 0, 0 , ),(222222y x y x y x xy y x f
在原点的可微性 .
这个例子说明,偏导存在不一定可微,(这一点与一元函数不同!)
(二)、充分条件
定理17.2(可微的充分条件)若函数),(y x f z =的偏导数在的某邻域内存在 , 且x f 和y f 在点) , (00y x 处连续 . 则函数f 在点) , (00y x 可微。
定理17.3(中值定理)设函数f 在点) , (00y x 的某邻域内存在偏导数 . 若),(y x 属于该邻域 , 则存在)(010x x x -+=θξ和)(020y y y -+=θη, 10 , 1021<<<<θθ, 使得
))( , ())( , (),(),(00000y y x f x x y f y x f y x f y x -+-=-ηξ. ( 证略 )
推论 若),(y x f y 在点) , (00y x 处连续, ),(y x f x 点) , (00y x 存在 , 则函数 f 在点) , (00y x 可微
证明: f y y x x f -?+?+) , (00) , (00y x
[][]) , () , () , () , (00000000y x f y x x f y x x f y y x x f -?++?+-?+?+=
0000( , )(,) 01, 0y x f x x y y y f x y x x θαθα=+?+??+?+?<<→ 0000(,)(,)y x f x y y f x y x x βα??=+?+?+??? 0→β y x y y x f x y x f y x ?+?+?+?=βα) , () , (0000.
即f 在点) , (00y x 可微
例6 ?????=+≠+++=.
0 , 0, 0 ,1sin )(),(22222222y x y x y x y x y x f
验证函数),(y x f 在点) 0 , 0 (可微 , 但x f 和y f 在点) 0 , 0 (处不连续 .
证明: ).0 , 0(),( , 01
sin )
,(2222→→++=y x y x y x y x f ρ
因此 )(),(ρο=y x f , 即 )(00)0,0(),(ρο+?+?=-y x f y x f ,
f 在点)0 , 0(可微 , 0)0,0( , 0)0,0(==y x f f . 但≠),(y x ) 0 , 0 (时, 有 2222221cos 1
sin 2),(y x y
x x y x x y x f x ++-+=, 沿方向,kx y = 202201||lim lim k x x y
x x
x x +=+→→不存在, ?沿方向,kx y = 极限 222201
cos lim y x y
x x x ++→不存在 ; 又→),(y x ) 0 , 0 (时, 01sin 222→+y x x ,因此, ),(lim )0,0(),(y x f x y x →不存在 , x f 在点) 0 , 0 (处不连续. 由f 关于x 和y 对称,y f 也在点) 0 , 0 (处不连续 .
(三)、连续、偏导数存在及可微之间的关系:
这三个概念之间的关系可以用下图表示(在),(00y x 点)
在上述关系中,反方向均不成立。下面以)0,0(),(00=y x 点为例,逐一讨论。
例1 ??
???=+≠++=0 ,00 ,),(222222y x y x y x xy y x f
这是教材中的典型例题,0)0,0()0,0(==y x f f 均存在,但),(y x f 在)0,0(点不可微,且),(lim 0
0y x f y x →→不存在,即),(y x f 在)0,0(点不连续。 例2 22),(y x y x f +=,这是上半圆锥,显然在)0,0(点连续,
)0,0(0),(lim 0
0f y x f y x ==→→, 但 ?
??<->===-0 ,10 ,1||)0,0()0,(2x x x x x x x f x f 故)0,0(x f 不存在。由y x ,的对称性,)0,0(y f 不存在。从而,),(y x f 在)0,0(点不可微(否则,)0,0(x f ,)0,0(y f 均存在)。
例3 ??
???=+≠+++=0 ,00 ,1sin )(),(22222222y x y x y x y x y x f 01sin lim )0,0()0,(lim )0,0(2200==-=→→x x x x f x f f x x x ,
由y x ,的对称性,0)0,0(=y f 。 22)0,0()0,0()0,0(),(y x y
f x f f y x f y x +---
01sin 1sin
)(222
2222
222→++=+++=y x y x y x y x y x (00→→y x ) 故),(y x f 在)0,0(点可微。且=)0,0(df +dx f x )0,0(0)0,0(=dy f y
??
???=+≠+++-+=0 ,00 ,1cos 21sin 2),(2222222222y x y x y x y x x y x x y x f x
取点列),(n n n y x P ,πn x n 21
=,0=n y ,显然))(0,0(),(∞→→n y x P n n n
)(2cos 22),(∞→-∞→-=n n n y x f n n x ππ
故),(lim 0
0y x f x y x →→不存在,从而),(y x f x 在)0,0(点不连续。由y x ,的对称性,),(y x f y
在)0,0(点也不连续。
对一元函数,可微与可导是等价的,即:可微?可导。但对二元函数,可微与偏导存在并不等价,即:可微?偏导存在,反之未必。应特别引起注意。
四 可微性的几何意义与应用
复习一元函数可微性的几何意义:切线引出二元函数可微性的几何意义、切平面。
定义(切平面)设P 是曲面S 上一点,II 为通过P 的一个平面,曲面S 上的动点Q 到P 和到平面H 的距离分别为 d 和h ,当Q 在S 上以任何方式趋于P 时,恒有0h d
→,则称平面II 为曲面S 在点P 处的切平面,P 为切点。 定理17.4曲面),(y x f z =在点)) , ( , , (0000y x f y x P 存在不平行于Z 轴的切平面的充要条件是函数),(y x f 在点),(000y x P 可微.
( 证略 )
全微分的几何意义
切平面的求法
设函数),(y x f 在点),(000y x P 可微 ,则曲面),(y x f z =在点)) , ( , , (0000y x f y x P 处的切平面方程为 ( 其中),(000y x f z = )
))(,())(,(0000000y y y x f x x y x f z z y x -+-=-,
法线方向数为 () 1 , ),( , ),( 0000-±y x f y x f y x ,
法线方程为 1
),(),(0000000--=-=-z z y x f y y y x f x x y x . 例1 试求抛物面 22by ax z +=在点),,(000z y x M 处的切平面方程和法线 方程 .
作近似计算和误差估计: 与一元函数对照, 原理 .
例2 求96.308.1的近似值.
例3 应用公式C ab S sin 2
1=计算某三角形面积 . 现测得50.12=a , 50.12=a ,8.30 ,b =30C =. 若测量b a , 的误差为C , 01.0±的误差为 1.0± . 求用此公式
计算该三角形面积时的绝对误差限与相对误差限.
作业 教材P117:1-13.
§2 复合函数微分法
教学目的 掌握复合函数求导的链式法则.
教学要求
(1)掌握复合函数求导的链式法则.
(2)掌握链式法则的证明和理解一阶全微分形式不变性.
教学建议
(1) 要求学生必须熟练掌握复合函数求导的链式法则,应布置较多习题以使学生能通过完成作业达到熟练使用链式法则的目的.
(2) 举例说明正确使用一阶全微分形式不变性的基本方法.
教学程序
一、 复合函数求导的链式法则
(一)、引言
Euclid 空间中点集的基本概念和基本定理;多元函数的极限论:极限与连续;多元函数微分学:偏导数与全微分的概念。进一步——多元函数微分学的相关知识。
从一个例子谈起:
例 )cos(xy x z ?=,
)sin()cos())sin(()cos(xy xy xy y xy x xy z x ?-=?-?+=,
).sin()sin(2xy x x xy x z y ?-=??-=
在上述计算中,是把z 作为x y 的函数且x y 是自变量。假如x y 不是自变
量,而是其它的变量函数,例如:v u x v u y +=-={,
此时,z 通过中间变量x, y 而成为u ,v 的函数,称为符合函数。问题是:如何求y x z z ,?
解决方案之一:求出z 关于u, v 的表达式,再求v u z z ,。即:
)2())sin()(()cos(2))sin()(()cos()
cos()(2222222222v v u v u v u z u
v u v u v u z v u v u z v u -?--++-=?--++-=-+=
试想,如果x, y 的表达式很复杂,这种方法可能会很困难!所以,我们有
必要寻找其它计算“所元函数的导数”的方法。为简单计,只解下述情形:
(,)(,,)(,,)z f x y x x s t u y y s t u =??=??=?
内。的某个开集定义在内,的值域在内,并且的某个开集定义在其中D R z D y x E R y x 23,, (二)、关于复合函数((,,),(,,))z f x s t u y s t u =关于,,s t u 的偏导数有下列结果:
定理1 (链式法则)设f 在点
00,x y D ∈()可微, 00000000(,,),(,,)x x s t u y y s t u ==。
又x 和y 都在点000(,,)s t u E ∈关于,,s t u 的偏导数存在,则在点000(,,)s t u 有
;;.z z x z y z z x z y z z x z y s x s y s t x t y t u x u y u
???????????????=?+?=?+?=?+???????????????? 注:(1) 几种特殊情形:定理1显然讲的是2个中间变量,3个自变量的情形,但其思想方法完全适用与其它情形:
1)设(,,),(,),(,),(,).u f x y z x x s t y y s t z z s t ====则
;u u x u y u z u u x u y u z s x s y s z s t x t y t z t
??????????????=?+?+?=?+?+??????????????? 2)设z y x u ,,,可微, (,),(),().u f x y x x t y y t ===则
u u x u y t x t y t
?????=?+?????? 3)设(,,),(,),(,).u f x y t x x s t y y s t ===则 u u x u y u zt s x s y s t s u u x u y u t t x t y t t t
???????=?+?+???????????????=?+?+???????? 例1 的二阶连续偏导数,和内有关于在设v u R v u f z 2),(=又设
x
y v y x u ==,2。求 。y z x z ????, (2) 计算复合函数的两阶偏导数,只要重复运用链式法则即可。如在例1中,求。y
x z y z x z ???????2
2222,, (3) 有时,为书写上方便,记
;),('1的偏导数关于第一个变量,即u v u f u
f f ??=
;),('2的偏导数关于第一个变量,即v v u f v f f ??= 22
'222'122'
11,v f f v u f f u f f ??=???=??=,。那么上面可写为: ''2''121222222''''''''111222124312;;442x y xx y z xyf f z x f f x x y y y z x y f f f yf f x x x =-
=+=-+++ 例2 22
,),,(dx dz dx dz e x f z f x
求二阶可微,设= 例3 .,,),2(2
22222
y x z y z x z d y x f z f ???????-=求二阶可微,设 (4)链式法则中的条件是充分的,并非必要的。在使用链式法则时,要注意f 的可微性条件,如果满足这一条件,链式法则不一定成立。
例: ???==≠?????=+==不可微。
在)0,0(),(0)0,0()0,0())0,0(,(,))0,0(,(,0),(2
22y x f f f y x y x y x y x y x f z y x 0(0,0)0(0,0)01,(,).2201010.
t t t t dz x y t z f t t dt z z x z y x x t y t =======?=?????=?+=?+?=?????若令则:但若用链式法则: 二、 一阶微分形式不变性
一阶微分有个很重要性质——形式不变性。在多元函数中也有类似的性质。
设),(y x f z =是二元可微函数,如果y x ,是自变量,则: .dy y
z dx x z dz ??+??= (dy dx ,各自独立数值) ()1
如果y x ,不是自变量而是中间变量,),,(),,(v u y y v u x x == 又设y x ,都可微,并且y x f ,,可以构成复合函数,那么:
dv v z du u z dz ??+??= 。
决定如上,由),,,,(.)()()()(
dv du v u dy dx dy y z dx x z dv v y du u y y z dv v x du u x x z v
y y z v x x z u y y z su x x z ??+??=??+????+??+????=????+?????+?????+?????= )
(2 由(1),(2)的dz 可知一阶微分形式的不变性。
注:(1)两阶微分设有这一性质,如下例
例5 设2,,.z x y x u v y u v =+==+ 2.z u v u v =++ 则
2222
22222224z z z d z du dudv dv vdu ududv u u v v ???=++=+???? 如果二阶微分只有形式不变性,则有:
22222222
2dy y z dxdy y x z dx x z z d ??+???+??= 但 00222222==??+???=??dz y
z y x z x z ,从而 (2)利用一阶微分形式不变性求偏导数
例6 设sin(),xy z e x y =+利用微分形式不变性求,dz 并求出
,.z z x y
???? 作业 教材P123: 1-5.
§3 方向导数与梯度
教学目的 掌握方向导数与梯度的定义,学会计算方向导数与梯度. 教学要求 掌握方向导数与梯度的定义,掌握方向导数与梯度的计算. 教学建议
(1) 适当介绍引入方向导数和梯度的意义(物理意义和计算方法上的意义).
(2) 对学生强调方向导数存在性与偏导数存在性和可微性的区别与联系. 教学程序
一、 方向导数:
(一)、方向导数的定义:
定义 设三元函数f 在点),,(0000z y x P 的某邻域)(0P ?3R 内有定义 . l 为从点0P 出发的射线 . ),,(z y x P 为l 上且含于)(0P 内的任一点 , 以ρ表示P 与0P 两点间的距离 . 若极限 ρρρρf P f P f l ?=-++→→000lim )()(lim
存在 , 则称此极限为函数f 在点0P 沿方向l 的方向导数 , 记为0P l f ?? 或
)(0P f l 、),,(000z y x f l . 对二元函数),(y x f z =在点),(000y x P , 可仿此定义方向导数 .
易见 x f ??、y f ?? 和 z
f ??是三元函数f 在点0P 分别沿X 轴正向、Y 轴正向和 Z 轴正向的方向导数 .
例1 ),,(z y x f =32z y x ++. 求f 在点0P ) 1 , 1 , 1 (处沿l 方向的方向导数,其中 (1) l 为方向) 1 , 2 , 2 (-; (2) l 为从点) 1 , 1 , 1 (到点) 1 , 2 , 2 (-的方向.
解 (1) l 为方向的射线为令===-=--=-1
12121z y x )0 ( >t . 即 ) 0 ( , 1 , 12 , 12≥+=+-=+=t t z t y t x . 3) 1, 1 , 1 ()(0==f P f , 37) 1 () 12 () 12 ( ) 1 , 12 , 12 ()(2332+++=+++-++=++-+=t t t t t t t t t f P f
t t t t z y x 3)2()2()1()1()1(222222=+-+=-+-+-=ρ.
因此 , .3
137lim )()(lim 230000=++=-=??++→→t t t t P f P f l f t P ρρ (2) 从点) 1 , 1 , 1 (到点) 1 , 2 , 2 (-的方向l 的方向数为), 0 , 3 , 1 (-l 方向的射线为 ) 0 ( , 1 , 13 , 1≥=+-=+=t z t y t x .
359) 1 , 13 , 1()(2+-=+-+=t t t t f P f , 3) 1, 1 , 1 ()(0==f P f ;
t t t z y x 10)3()1()1()1(22222=-+=-+-+-=ρ.
因此 , .105
1059lim )()(lim 20000-=-=-=??++→→t t t P f P f l f t P ρρ
(二)、 方向导数的计算:
定理: 若函数f 在点),,(0000z y x P 可微 , 则f 在点0P 处沿任一方向l 的方向导数都存在 , 且
=)(0P f l )(0P f x αcos +)(0P f y βcos +)(0P f z γcos ,
其中αcos 、βcos 和γcos 为l 的方向余弦.
( 证 ) 对二元函数),(y x f , =)(0P f l )(0P f x αcos +)(0P f y βcos , 其中α和β是l 的方向角.
注: 由=)(0P f l )(0P f x αcos +)(0P f y βcos +)(0P f z γcos
=()(0P f x ,)(0P f y ,)(0P f z (αcos ,βcos , γcos ), 可见 , )(0P f l 为向量()(0P f x , )(0P f y , )
(0P f z )在方向l 上的投影. 例2 ( 上述例1 )
解 (1) l 的方向余弦为αcos =321)2(22222=
+-+, βcos =32-, γcos =3
1. )(0P f x =1 , )(0P f y =221==y y , )(0P f z =3312
==z z . 因此 , l f ??=)(0P f x αcos +)(0P f y βcos +)(0P f z γcos =3
1313) 32(232=?+-?+.
(2) l 的方向余弦为
αcos =101)11()12()12(1
2222=-+--+--, βcos =103
-, γcos =0 .
因此 , l f ??=10
510321011-=?-?. 可微是方向导数存在的充分条件 , 但不必要 .
二、 梯度 ( 陡度 ):
(一)、梯度的定义: =gradf ()(0P f x , )(0P f y , )
(0P f z ) . ||gradf = ()()()202020)()()(P f P f P f z y x ++.
易见 , 对可微函数f , 方向导数是梯度在该方向上的投影.
(二)、 梯度的几何意义: 对可微函数 , 梯度方向是函数变化最快的方向 . 这是因为
=)(0P f l =?l gradf ||)(0P gradf θcos .
其中θ是l 与)(0P gradf 夹角. 可见0=θ时)(0P f l 取最大值 , 在l 的反方向取最小值 .
(三)、梯度的运算:
1 grad =+)(c u grad u .
2 grad (αu +βv ) = αgrad u +βgrad v .
3 grad (u v ) = u grad v +v grad u .
4 grad 2
u vgradu ugradv u v -=. 5 grad f (u ) = gradu u f )('.
证: 4 2u v u uv u v x x x -=??? ?? , 2u v u uv u v y y y
-=??? ??. grad =--=) , (12v u uv v u uv u
u v y y x x []
=-=) , ( ) , (12v u v u v u uv u y x y x
[]
=-=) , () , (12y x y x u u v v v u u 2u vgradu ugradv -. 总结:gradf 的方向表示数量场f 在l 分三元沿此方向的方向导数达到最大;gradf 的根长就是这个最大的方向导数。
作业 教材 P127 1-7
§4 泰勒公式与极值问题
教学目的 掌握二元函数的高阶偏导数与泰勒公式的定义,掌握二元函数的极值的必要条件与充分条件.
教学要求
(1)掌握二元函数的高阶偏导数与泰勒公式的定义,能够根据二元函数的极值的必要条件与充分条件寻找二元函数的极值与最大(小)值.
(2)掌握混合偏导数与求导次序无关的定理的证明以及二元函数的极值的必要条件充分条件定理的证明.
教学建议
(1) 布置适量的求二元函数的高阶偏导数和求二元函数的极值与最值的习题.
(2) 讨论混合偏导和与求导次序无关的多种定理证明的习题有一定的难度,只对较好学生布置有关习题.
教学程序
一、中值定理:
定理 设二元函数f 在凸区域D 2R ?上连续 , 在D 的所有内点处可微 . 则对D 内任意两点int ) , ( , ),(∈++k b h a Q b a P D , 存在) 10 ( <<θθ, 使 k k b h a f h k b h a f b a f k b h a f x ) , () , (),() , (θθθθ+++++=-++. 证: 令()( , ) , t f a th b tk Φ=++然后利用一元函数的中值定理.
推论 若函数f 在区域D 上存在偏导数 , 且x f ≡y f ≡0, 则f 是D 上的常值函数.
二、 Taylor 公式:
定理 (Taylor 公式) 若函数f 在点),(000y x P 的某邻域)(0P 内有直到1+n 阶连续偏导数 , 则对)(0P 内任一点) , (00k y h x ++,存在相应的) 1 , 0(∈θ, 使
∑=+++???? ????+??++???? ????+??=
++n i n i k y h x f y k x h n y x f y k x h i k y h x f 00010000). , ()!1(1),(!1 ) , (θθ
证 略
例1 求函数y x y x f =),(在点) 4 , 1 (的Taylor 公式 ( 到二阶为止 ) . 并用它计算 .) 08.1 (96.3
三、 极值问题:
(一)、极值的定义: 注意只在内点定义极值.
(二)、极值的必要条件:与一元函数比较 .
定理 设0P 为函数)(P f 的极值点 . 则当)(0P f x 和存在时 , 有 )(0P f x =)(0P f y 0=. ( 证 )
函数的驻点、不可导点 , 函数的可疑点 .
(三)、极值的充分条件:
代数准备: 给出二元( 实 )二次型 222),(cy bxy ax y x g ++=. 其矩阵为
???
? ??c b b a .
1 ),(y x g 是正定的,? 顺序主子式全0 >,
),(y x g 是半正定的,? 顺序主子式全 0 ≥;
2 ),(y x g 是负定的,? 0||) 1(1>-k ij k a , 其中k ij a 1
||为k 阶顺序主子式. ),(y x g 是半负定的, ? 0||) 1(1≥-k ij k a .
3 ???
? ??c b b a < 0时, ),(y x g 是不定的.
充分条件的讨论 设函数),(y x f 在点),(000y x P 某邻域有二阶连续偏导数 . 由Taylor 公式 , 有
)()(!21)(),() , (202
00000ρ +???? ????+??+???? ????+??=-++P f y k x h P f y k x h y x f k y h x f
=)(0P f x h +)(0P f y k + []
)()()(2)(!21220020ρ +++k P f hk P f h P f yy xy xx . 令 )(0P f A xx = , )(0P f B xy =, )(0P f C yy =, 则当0P 为驻点时, 有[]
)(221),() , (2220000ρ +++=-++Ck Bhk Ah y x f k y h x f . 其中22k h +=ρ. 可见式),() , (0000y x f k y h x f -++的符号由二次型222Ck Bhk Ah ++完全决定.
称该二次型的矩阵为函数),(y x f 的Hesse 矩阵. 于是由上述代数准备, 有
1 0 , 02>->B AC A , 0 P ?为 ( 严格 ) 极小值点 ;
2 0 , 02>-
3 0 2<-B AC 时, 0P 不是极值点;
4 0 2=-B AC 时, 0P 可能是极值点 , 也可能不是极值点 .
综上 , 有以下定理 :
定理 设函数)(P f 在点0P 的某邻域内有连续的二阶偏导数 , 0P 是驻点 . 则
1 ()0)( , 0)(020>->P f f f P f xy yy xx xx 时 , 0P 为极小值点;
2 ()0)( , 0)(020>-
3 ()0)( 02<-P f f f xy yy xx 时 , 0P 不是极值点;
4 ()
0)( 02=-P f f f xy yy xx 时 , 0P 可能是极值点 , 也可能不是极值点 . 四、 函数的最值:
例8 求函数
),(y x f y x y xy x 4102422+--+=
在域D = } 4 , 0 , 0 |),( {≤+≥≥y x y x y x 上的最值 .
解 令 ???=+-==-+=.04 44),(,01042),(y x y x f y x y x f y
x 解得驻点为) 2 , 1 (. 1) 2 , 1 (-=f . 在边界) 40 ( 0≤≤=y x 上 , y y y f 42),0(2+-=, 驻点为1=y ,
2)1,0(=f ;
在边界) 40 ( 0≤≤=x y 上 , x x x f 10)0,(2-=, 没有驻点; 在边界) 40 ( 4≤≤-=x x y 上 , 16185)4 , (2-+-=-x x x x f , 驻点为8.1=x , 2.0)8.14 , 8.1(=-f .
又24)0,4( , 16)4,0( , 0)0,0(-=-==f f f .
于是 , ==)}0,4( , )4,0( , )0,0( , )2.2 , 8.1( , )1,0( , )2,1(max{),(max f f f f f f y x f D
2.0} 24 , 16 , 0 , 2.0 , 2 , 1 max{=---=. ),(min y x f D
24} 24 , 16 , 0 , 2.0 , 2 , 1 min{-=---=. 作业 教材P140-141:1-11
多元函数微分学知识点梳理
第九章 多元函数微分学 内容复习 一、基本概念 1、知道:多元函数的一些基本概念(n 维空间,n 元函数,二重极限,连续等);理解:偏导数;全微分. 2、重要定理 (1)二元函数中,可导、连续、可微三者的关系 偏导数连续?可微???函数偏导数存在 ?连续 (2)(二元函数)极值的必要、充分条件 二、基本计算 (一) 偏导数的计算 1、 偏导数值的计算(计算),(00y x f x ') (1)先代后求法 ),(00y x f x '=0),(0x x y x f dx d = (2)先求后代法(),(00y x f x '=00),(y y x x x y x f ==') (3)定义法(),(00y x f x '=x y x f y x x f x ?-?+→?),(),(lim 00000)(分段函数在分段点处的偏导数) 2、偏导函数的计算(计算(,)x f x y ') (1) 简单的多元初等函数——将其他自变量固定,转化为一元函数求导 (2) 复杂的多元初等函数——多元复合函数求导的链式法则(画树形图,写求导公式) (3) 隐函数求导 求方程0),,(=z y x F 确定的隐函数),(y x f z =的一阶导数,z z x y ???? ,,,(),,y x z z F F z z x y z x F y F x y x y z ''???=-=-?''????? 公式法:(地位平等)直接法:方程两边同时对或求导(地位不平等) 注:若求隐函数的二阶导数,在一阶导数的基础上,用直接法求。 3、高阶导数的计算 注意记号表示,以及求导顺序 (二) 全微分的计算 1、 叠加原理
第七章 多元函数的微分学
第七章多元函数的微分学 一、多元函数微分学网络图 二、内容与要求 1.理解多元函数的概念,理解二元函数的几何意义。 2.了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质。 3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和充分条件, 了解全微分形式的不变性。
4.掌握多元复合函数一阶、二阶偏导数的求法。 5.会求多元隐函数的偏导数。 6.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件, 了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值, 会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题。 重点多元函数偏导数和全微分的概念,多元复合函数一阶、二阶偏导数的求法。用拉格朗日乘数法求条件极值,求简单多元函数的最大值和最小值,解决一些简单的应用问题。 难点多元复合函数二阶偏导数的求法。用拉格朗日乘数法求条件极值,求简单多元函数的最大值和最小值,解决一些简单的应用问题。 三、概念、定理的理解与典型错误分析 1.求多元函数极限的方法 (1)利用初等多元函数的连续性,即若是初等函数,在的定义域中,则 注:所谓的初等多元函数就是用一个数学表达式给出的解析式. (2)利用多元函数极限的四则运算。 (3)转化为一元函数的极限,利用一元函数的极限来计算. (4)对于证明或求时,感觉极限可能时零, 而直接又不容易证明或计算,这时可用夹逼定理,即而 由夹逼定理知从而 2.判断多元函数极限不存在的方法 (1)选取两条特殊的路径,而函数值的极限存在,但不相等,则不存在。
注意: 与的区别,前面两个本质是两次求一元函数的极限, 我们称为求累次极限,而最后一个是求二元函数的极限,我们称为求二重极限。 例1 而知不存在. 例2 在原点的两个累次极限都不存在,但是 由于,因此. 由例1知两个累次极限存在,但二重极限不存在,由例2知两个累次极限不存在, 但二重极限存在,但我们有下面的结论。 定理7。1 若累次极限和二重极限都存在,则三者相等。 (2)推论。若存在且不相等,则不存在。 3.求多元函数的偏导数
第十七章多元函数微分学习题课
第十七章 多元函数微分学习题课 一 疑难问题与注意事项 1.(,)z f x y =在),(000y x P 可微的等价定义: 1)0000(,)(,)()z f x x y y f x y A x B y o ρ?=+?+?-=?+?+,0 () lim 0o ρρρ →=; 2)00000 [(,)(,)] lim 0x y z f x y x f x y y ρρ →?-?+?=; 3), y x y B x A z ?+?+?+?=?βα()() ()() ,0,0,0,0lim lim 0x y x y αβ??→??→= =. 2.求(,)f x y 在00(,)x y 处的偏导数方法小结: 答 1)利用定义求(主要适用于分段函数的分段点处的偏导数): 0000000 (,)(,) (,)lim x x f x x y f x y f x y x ?→+?-=?, 0000000 (,)(,) (,)lim y y f x y y f x y f x y y ?→+?-=?. 2)转化为一元函数的导数: ()0 000,(,)x x x df x y f x y dx ==,() 000,(,)y y y df x y f x y dy == . 例如,2(,)(f x y x y =+-(1,1)x f . 解 () ()211 ,1(1,1)2x x x d x df x f dx dx ==== =. 3)先求偏导函数,在代值,即 ()0 00(,)(,),x x x y f x y f x y =,0 00(,) (,)(,)y y x y f x y f x y =. 3.求(,)z f x y =(初等函数不含分段点)的偏导函数方法小结: 答 1)求 z x ??,把y 当常数,对x 求导,求z y ??,把x 当常数,对y 求导. 2)运用轮换性,若在(,)z f x y =中,把x 换成y , y 换成x ,(,)z f x y =不变,则称(,)z f x y =关于x 和y 具有轮换性.若已经求出 z x ??,只要在z x ??把x 换成y , y 换成x ,
数学分析教案_(华东师大版)第十七章__多元函数微分学
第十七章多元函数微分学 教学目的:1.理解多元函数微分学的概念,特别应掌握偏导数、全微分、连续及 偏导存在、偏导连续等之间的关系;2.掌握多元函数特别是二元函数可微性及其应用。 教学重点难点:本章的重点是全微分的概念、偏导数的计算以及应用;难点是复合函数偏导数的计算及二元函数的泰勒公式。 教学时数:18学时 § 1 可微性 一.可微性与全微分: 1.可微性:由一元函数引入. 亦可写为, 时. 2.全微分: 例1 考查函数在点处的可微性 . P107例1 二.偏导数: 1.偏导数的定义、记法: 2.偏导数的几何意义: P109 图案17—1.
3.求偏导数: 例2 , 3 , 4 . P109—110例2 , 3 , 4 . 例5. 求偏导数. 例6. 求偏导数. 例7. 求偏导数, 并求. 例8. 求和. 解=, =. 例9 证明函数在点连续 , 并求和. 证 . 在点连续 . ,
不存在 . 三.可微条件: 1.必要条件: Th 1 设为函数定义域的内点.在点可微 , 和存在 , 且 . ( 证 ) 由于, 微分记为 . 定理1给出了计算可微函数全微分的方法. 两个偏导数存在是可微的必要条件 , 但不充分. 例10考查函数 在原点的可微性 . [1]P110 例5 . 2.充分条件:
Th 2 若函数的偏导数在的某邻域内存在 , 且和在点处连续 . 则函数在点可微 . ( 证 ) P111 Th 3 若在点处连续, 点存在 , 则函数在点可微 . 证 . 即在点可微 . 要求至少有一个偏导数连续并不是可微的必要条件 . 例11 验证函数在点可微 , 但和在点处不连续 . (简证,留为作业) 证
高等数学习题详解-第7章 多元函数微分学
1. 指出下列各点所在的坐标轴、坐标面或卦限: A (2,1,-6), B (0,2,0), C (-3,0,5), D (1,-1,-7). 解:A 在V 卦限,B 在y 轴上,C 在xOz 平面上,D 在VIII 卦限。 2. 已知点M (-1,2,3),求点M 关于坐标原点、各坐标轴及各坐标面的对称点的坐标. 解:设所求对称点的坐标为(x ,y ,z ),则 (1) 由x -1=0,y +2=0,z +3=0,得到点M 关于坐标原点的对称点的坐标为:(1,-2,-3). (2) 由x =-1,y +2=0,z +3=0,得到点M 关于x 轴的对称点的坐标为:(-1,-2,-3). 同理可得:点M 关于y 轴的对称点的坐标为:(1, 2,-3);关于z 轴的对称点的坐标为:(1,-2,3). (3)由x =-1,y =2,z +3=0,得到点M 关于xOy 面的对称点的坐标为:(-1, 2,-3). 同理,M 关于yOz 面的对称点的坐标为:(1, 2,3);M 关于zOx 面的对称点的坐标为:(-1,-2,3). 3. 在z 轴上求与两点A (-4,1,7)和B (3,5,-2)等距离的点. 解: 设所求的点为M (0,0,z ),依题意有|MA |2=|MB |2,即 (-4-0)2+(1-0)2+(7-z)2=(3-0)2+(5-0)2+(-2-z)2. 解之得z =11,故所求的点为M (0,0, 149 ). 4. 证明以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 解:由两点距离公式可得2 12 14M M =,2 2 13236,6M M M M == 所以以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 5. 设平面在坐标轴上的截距分别为a =2,b =-3,c =5,求这个平面的方程. 解:所求平面方程为1y x z ++=。 6. 求通过x 轴和点(4,-3,-1)的平面方程. 解:因所求平面经过x 轴,故可设其方程为 Ay +Bz =0. 又点(4,-3,-1)在平面上,所以-3A -B =0.即B=-3 A 代入并化简可得 y -3z =0. 7. 求平行于y 轴且过M 1(1,0,0),M 2(0,0,1)两点的平面方程. 解:因所求平面平行于y 轴,故可设其方程为 Ax +Cz +D =0. 又点M 1和M 2都在平面上,于是 0A D C D +=?? +=? 可得关系式:A =C =-D ,代入方程得:-Dx -Dz +D =0. 显然D ≠0,消去D 并整理可得所求的平面方程为x +z -1=0. 8. 方程x 2+y 2+z 2-2x +4y =0表示怎样的曲面? 解:表示以点(1,-2,0 9. 指出下列方程在平面解析几何与空间解析几何中分别表示什么几何图形? (1) x -2y =1; (2) x 2+y 2=1; (3) 2x 2+3y 2=1; (4) y =x 2. 解:(1)表示直线、平面。(2)表示圆、圆柱面。(3)表示椭圆、椭圆柱面。 (4)表示抛物线、抛物柱面。
多元函数微分学习题
6 .函数 在点 处具有两个偏导数 是函数存在全 第五部分 多元函数微分学( 1) (x,y) (0,0) 在点 (0,0)处 ( ) (x,y) (0,0) xuv 3.设函数 u u(x, y), v v(x, y) 由方程组 2 2 确定,则当 u y u 2 v 2 4.设 f (x, y)是一二元函数, (x 0,y 0) 是其定义域的一点, 则下列命题中一定正确的是 ( ) (A) 若 f (x,y)在点 (x 0,y 0) 连续,则 f (x,y)在点(x 0,y 0)可导。 (B) 若 f(x,y)在点 (x 0,y 0)的两个偏导数都存在,则 f(x,y)在点 (x 0,y 0)连续。 (C) 若 f(x,y)在点 (x 0,y 0)的两个偏导数都存在,则 f(x,y)在点 (x 0,y 0)可微。 (D) 若 f (x,y)在点 (x 0,y 0) 可微,则 f (x,y)在点(x 0,y 0)连续。 答:D 3 x 2 y 2 z 2 在点 (1, 1,2) 处的梯度是 ( ) 1 1 2 1 1 2 1 1 2 (A) ( , , ) (B) 2( , , ) (C) ( , , ) (D) 3 3 3 3 3 3 9 9 9 答:A [ 选择题 ] x 3y 2z 1 0 1 .设有直线 及平面 2x y 10z 3 0 容易题 1— 36,中等题 37—87,难题 88— 99。 。 (C) 垂直于 4x 2y z 2 0 ,则直线 L ( ) (A) 平行于 。 (B) 在上 答:C (D) 与 斜交。 (A) 连续,偏导数存在 (B) (C) 不连续,偏导数存在 (D) 答:C 连续,偏导数不存在 不连续,偏导数不存在 (A) x (B) v (C) u (D) uv uv uv 答:B y uv 2.二元函数 f (x,y) xy , 2 2 , xy 0, 5.函数 f(x,y,z) x ( )
高数多元函数微分学教案 第五讲 隐函数的求导公式
第五讲 隐函数的求导公式 授课题目: §8.4 隐函数的求导公式 教学目的与要求: 会求隐函数(包括由两个方程组成的方程组确定的隐函数)的偏导数。 教学重点与难点: 重点:求由一个方程确定的隐函数的偏导数。 难点:求隐函数(包括由两个方程组成的方程组确定的隐函数)的偏导数。 讲授内容: 一、一个方程的情形 隐函数存在定理1 设函数F (x , y )在点P (x 0, y 0)的某一邻域内具有连续偏导数, F (x 0, y 0)=0, F y (x 0, y 0)≠0, 则方程F (x , y )=0在点(x 0, y 0)的某一邻域内恒能唯一确定一个连续且具有连续导数的函数y =f (x ), 它满足条件y 0=f (x 0), 并有 y x F F dx dy -=. (2) 公式(2)的推导:将y =f (x )代入F (x , y )=0, 得恒等式 F 【x , f (x )】≡0, 等式两边对x 求导得 0=???+??dx dy y F x F , 由于F y 连续, 且F y (x 0, y 0)≠0, 所以存在(x 0, y 0)的一个邻域, 在这个邻域同F y ≠0, 于是得 y x F F dx dy -= 例1 验证方程x 2+y 2-1=0在点(0, 1)的某一邻域内能唯一确定一个有连续导数、当x =0时y =1的隐函数y =f (x ), 并求这函数的一阶与二阶导数在x =0的值. 解 设F (x , y )=x 2+y 2-1, 则F x =2x , F y =2y , F (0, 1)=0, F y (0, 1)=2≠0. 因此由
第7章 多元函数微分学
§7.1 空间解析几何基本知识 教学内容提要 1. 空间直角坐标系; 2. 空间两点间的距离公式与两点连线的中点坐标公式; 3. 简单的曲面方程。 教学目的与要求 1. 了解空间直角坐标系和空间两点间的距离公式及两点连线的中点公式; 2. 了解常用二次曲面的方程及其图形。 教学重点与难点 常用二次曲面的方程及其图形的简单描绘. 教学时数 4 教学过程: 一、空间直角坐标系 1.空间直角坐标系的建立 过空间定点0,作三条互相垂直的数轴,他们都以0为原点 且一般具有相同的长度单位。这三条轴分别称为x 轴,y 轴, z 轴,统称坐标轴。通常把x 轴和y 轴配置在水平面上,z 轴 z 在铅垂方向,他们的指向符合右手法则. 2、空间两点间的距离公式 空间任意两点),,(1111z y x M 和),,(2222z y x M 21221221221)()()(z z y y x x M M -+-+-= 特殊地,点),,(z y x M 与坐标原点)0,0,0(O 的距离为222z y x OM ++= 。 例1 在z 轴求与两点)7,1,4(-A 和)25,3(-B 等距离的点的坐标。 二、曲面及其方程的概念 1.曲面方程 在空间解析几何中,任何曲面都可以看作满足一定条件的点的几何轨迹 ,如果曲面S 上任一点的坐标都满足方程0),,(=z y x F ,不在曲面S 上的点的坐标都不满足该方程,则称此方程0),,(=z y x F 为曲面的方程,而曲面S 就叫做方程的图形。 例2 动点),,(z y x P 与两定点)1,3,2(),0,2,1(21-P P 的距离相等,求此动点P 的轨迹。 三、几种常见的曲面及其方程 1、平面的一般方程 任一平面都可以用三元一次方程来表示 .任一三元一次方程Ax +By +Cz +D =0的图形总是一个平面. 例3 求通过x 轴和点(4, -3, -1)的平面的方程. 解 平面通过x 轴, 一方面表明它的法线向量垂直于x 轴, 即A =0; 另一方面表明 它必通过原点, 即D =0. 因此可设这平面的方程为
第五章-多元函数微分学习题参考答案
第五章多元函数微分学习题 练习5.1 1.在空间直角坐标系下,下列方程的图形是什么形状? (1) )(422 2 椭圆抛物面z y x =+ (2) 圆锥面)(4222z y x =+ (3) 椭球面)(19 164222=++z y x (4) 圆柱面)(12 2=+z x 2.求下列函数的定义域: (1)y x z --= 解:?? ?≥-≥0 y x y 即?? ? ??≥≥≥y x x y 200 ∴函数的定义域为{ }y x y x y x ≥≥≥2,0,0|),( (2) z =解:0≥-y x {}0|),(≥-∴y x y x 函数的定义域为 3. ()y x f ,对于函数= y x y x +-,证明不存在),(lim 0y x f x → 分析:由二元函数极限定义,我们只须找到沿不同路径0(0,0)p p →时,所 得极限值不同即可。 证明: ①(,)0,0)(0,0)p x y x x y p ≠=0当沿轴(此时趋于时, (,)(,0)1,lim (,)1x y f x y f x f x y →→=== ②当0(,)(0)00p x y y kx k p =≠沿直线趋于(,)时, 0011(,)lim (,)1(0)11x y x kx k k f x y f x y k x kx k k →→---= ==≠≠+++
综合①②可知函数极限不存在,证毕。 练习5.2 1.求下列函数的偏导数 ①;,,33y z x z xy y x z ????-=求 解: 23323,3xy x y z y y x x z -=??-=?? ②;,,)ln(y z x z xy z ????=求 解:[]1 211ln() 2z xy y x xy -?=??=? []1 211ln() 2z xy x y xy - ?=??=? ③222ln(),,z z z x x y x x y ??=+???求 解: 1ln()z x y x x x y ?=++??+ 2222)(2)(1))(ln()(y x y x y x x y x y x y x x y x x x z x x z ++= +-+++=+++??=????=?? 222 1()(ln())()()z z x x y x y x y y x y x y x y x y x y ????==++=-=?????++++ ④;,3z y x u e u xyz ????=求 解;2 2,()xyz xyz xyz xyz u u yze ze yzxze z xyz e x x y ??==+=+??? 3222()(())(12)()xyz xyz xyz u u z xyz e xyz e z xyz xye x y z z x y z ????==+=+++???????
第九章多元函数微分法及其应用教案
第九章多元函数微分法及其应用 【教学目标与要求】 1、理解多元函数的概念和二元函数的几何意义。 2、了解二元函数的极限与连续性的概念,以及有界闭区域上的连续函数的性质。 3、理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和充分条件, 了解全微分形式的不变性。 4、理解方向导数与梯度的概念并掌握其计算方法。 5、掌握多元复合函数偏导数的求法。 6、会求隐函数(包括由方程组确定的隐函数)的偏导数。 7、了解曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程。 8、了解二元函数的二阶泰勒公式。 9、理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格郎日乘数法求条件极值,会求简多元函数的最大值和最小值,并会解决一些简单的应用问题。 【教学重点】 1、二元函数的极限与连续性; 2、函数的偏导数和全微分; 3、方向导数与梯度的概念及其计算; 4、多元复合函数偏导数; 5、隐函数的偏导数;多元函数极值和条件极值的求法; 6、曲线的切线和法平面及曲面的切平面和法线; 【教学难点】 1、二元函数的极限与连续性的概念; 2、全微分形式的不变性; 3、复合函数偏导数的求法; 4、二元函数的二阶泰勒公式; 5、隐函数(包括由方程组确定的隐函数)的偏导数; 6、拉格郎日乘数法,多元函数的最大值和最小值。 【教学课时分配】 (18学时) 第1 次课§1第2 次课§2 第3 次课§3 第4 次课§4 第5次课§5 第6次课§6 第7次课§7 第8次课§8 第9次课习题课 【参考书】 [1]同济大学数学系.《高等数学(下)》,第五版.高等教育出版社. [2] 同济大学数学系.《高等数学学习辅导与习题选解》,第六版.高等教育出版社. [3] 同济大学数学系.《高等数学习题全解指南(下)》,第六版.高等教育出版社
多元函数微分学及其应用
第8章 多元函数微分学及其应用 参考解答 1、设22 , y f x y x y x ??+=- ??? ,求(),f x y ,(),f x y xy -。 解:()()()()2 21, 1y y x y x f x y x y x y x y x y y x x y x - -??+=+-=+=+ ?+? ? + ,故得 ()2 1,1y f x y x y -=+,()()21,1xy f x y xy x y xy --=-+ 2、求下列各极限: 2242222 2220000 cos sin 1(1) lim lim lim sin 204x r r y x y r r x y r θθθ→→→→===+ 注意:在利用极坐标变换cos , sin x r y r θθ==来求极限时,θ也是变量。本题中,0r →时,2r 为无穷小量,而2 sin 2θ为有界变量,故所求极限为零。 ()00sin sin (2) lim lim 1x t y a xy t xy t →→→== 3、证明极限2 2400 lim x y xy x y →→+不存在。 证明:当2 y kx =时,()2242,1xy k f x y x y k ==++,故2 22420 lim 1y kx x xy k x y k =→=++与k 有关。可见,(),x y 沿不同的路径趋于()0,0时,函数极限不同,故极限不存在。(两路径判别法) 4、讨论下列函数在()0,0点处的连续性: (1)()()()222222 22 ln , 0 ,0, 0 x y x y x y f x y x y ?+++≠?=?+=?? 解: ()() ()()() ()()()2 222,0,0,0,0 lim ,lim ln lim ln 00,0x y x y t f x y x y x y t t f →→→= ++=== 故原函数在()0,0点处连续。
高数多元函数微分学教案 第一讲 多元函数的基本概念
第八章 多元函数微分法及其应用 第一讲 多元函数的基本概念 授课题目: §8.1多元函数的基本概念 教学目的与要求: 1、理解多元函数的概念. 2、了解二元函数的极限与连续性的概念,以及有界闭区域上连续函数的性质. 教学重点与难点: 重点:多元函数的概念、二元函数的极限和连续的概念. 讲授内容: 一、平面点集 n 维空间 1、平面点集 平面上一切点的集合称为二维空间, 记为R 2 即 R 2=R ?R={(x , y ):x , y ∈R } 坐标平面上具有某种性质P 的点的集合, 称为平面点集,记作 E ={(x , y ):(x , y )具有性质P }. 例如,平面上以原点为中心、r 为半径的圆内所有点的集合是 C ={(x , y ):x 2+y 2 如果不需要强调邻域的半径δ, 则用U (P 0)表示点P 0的某个邻域, 点P 0的去心邻域记作)(0P U .. 点与点集之间的关系: 任意一点P ∈R 2与任意一个点集E ?R 2之间必有以下三种关系中的一种: (1)内点:如果存在点P 的某一邻域U (P ), 使得U (P )?E , 则称P 为E 的内点. (2)外点:如果存在点P 的某个邻域U (P ), 使得U (P )?E =?, 则称P 为E 的外点. (3)边界点:如果点P 的任一邻域内既有属于E 的点, 也有不属于E 的点, 则称P 点为E 的边点. E 的边界点的全体, 称为E 的边界, 记作?E . E 的内点必属于E ; E 的外点必定不属于E ; 而E 的边界点可能属于E , 也可能不属于E . (4)聚点:如果对于任意给定的δ>0, 点P 的去心邻域),(δP U 内总有E 中的点, 则称P 是E 的聚点. 由聚点的定义可知, 点集E 的聚点P 本身, 可以属于E , 也可能不属于E . 例如, 设平面点集E ={(x , y )|1 第八章多元函数微分法及其应用 教学目的: 1、理解多元函数的概念和二元函数的几何意义。 2、了解二元函数的极限与连续性的概念,以及有界闭区域上的连续函数的性质。 3、理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和充分条件,了解全微分形式的不变性。 4、理解方向导数与梯度的概念并掌握其计算方法。 5、掌握多元复合函数偏导数的求法。 6、会求隐函数(包括由方程组确定的隐函数)的偏导数。 7、了解曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程。 8、了解二元函数的二阶泰勒公式。 9、理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格郎日乘数法求条件极值,会求简多元函数的最大值和最小值,并会解决一些简单的应用问题。 教学重点: 1、二元函数的极限与连续性; 2、函数的偏导数和全微分; 3、方向导数与梯度的概念及其计算; 4、多元复合函数偏导数; 5、隐函数的偏导数 6、曲线的切线和法平面及曲面的切平面和法线; 7、多元函数极值和条件极值的求法。 教学难点: 1、二元函数的极限与连续性的概念; 2、全微分形式的不变性; 3、复合函数偏导数的求法; 4、二元函数的二阶泰勒公式; 5、隐函数(包括由方程组确定的隐函数)的偏导数; 6、拉格郎日乘数法; 7、多元函数的最大值和最小值。 §8. 1 多元函数的基本概念 一、平面点集n 维空间 1.平面点集 由平面解析几何知道, 当在平面上引入了一个直角坐标系后, 平面上的点P 与有序二元实数组(x , y )之间就建立了一一对应. 于是, 我们常把有序实数组(x , y )与平面上的点P 视作是等同的. 这种建立了坐标系的平面称为坐标平面. 二元的序实数组(x , y )的全体, 即R 2=R ?R ={(x , y )|x , y ∈R }就表示坐标平面. 坐标平面上具有某种性质P 的点的集合, 称为平面点集, 记作 E ={(x , y )| (x , y )具有性质P }. 例如, 平面上以原点为中心、r 为半径的圆内所有点的集合是 C ={(x , y )| x 2+y 2 多元函数微分学总结内部编号:(YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128) `第八章多元函数微分学 基本知识点要求 1.理解多元函数的概念,理解二元函数的几何意义. 2.了解二元函数的极限与连续的概念以及有界闭区域上连续函数的性质。 3.理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和充分条件,了解全微分形式的不变性。 4.理解方向导数与梯度的概念,并掌握其计算方法. 5.熟练掌握多元复合函数一阶、二阶偏导数的求法. 6.了解隐函数存在定理,熟练掌握多元隐函数偏导数的求法. 7.了解空间曲线的切线和法平面及曲面的切平面和法线的概念,熟练掌握它们的方程的求法。 8.了解二元函数的二阶泰勒公式. 9.理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,掌握二元函数极值存在的充分条件,并会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题。 基本题型及解题思路分析 题型1 与多元函数极限、连续、偏导数和可微的概念及其之间的关系有关的题 1.二元函数的极限与连续的概念及二元函数极限的计算。 (1)基本概念 ①二元函数极限的定义:设()(,)f P f x y =的定义域为D ,000(,)P x y 是D 的聚点.若?常数A ,对于?0ε>,总?0δ>,使得当0(,)(,)P x y D U P δ∈时,都有 ()(,)f P A f x y A ε-=-<成立,则称A 为函数(,)f x y 当00(,)(,)x y x y →时的极限,记 作 000 (,)(,) lim (,)lim ()x y x y P P f x y A f P A →→==或。 ②二元函数的连续:设()(,)f P f x y =的定义域为D ,000(,)P x y 为D 的聚点,且 0P D ∈.若 0000(,)(,) lim (,)(,)x y x y f x y f x y →=,则称(,)f x y 在点000(,)P x y 连续。 (2)关于二元函数极限的解题思路 注意:在二元函数0 lim ()P P f P A →=存在的定义中,0P P →方式任意,正是由于这 一点致使二元函数有与一元函数不一样的性态,在学习过程中注意比较、总结和体会二者之间的不同。 ① 证明二元函数的极限不存在:若0P P 以两种不同的方式趋于时,()f P 的极 限不同,则0 lim ()P P f P →一定不存在(见例1)。 ②求二元函数的极限:可以应用一元函数求极限方法中的适用部分求二元 函数的极限,比如:极限的局部有界性、局部保号性、四则运算法则、夹逼准则、两个重要的极限、变量代换法则、等价无穷小代换、分子分母有理化、无穷小量与有界变量的乘积仍为无穷小量、连续性等(见例2) 例1证明:2 24(,)xy f x y x y =+在原点0,0()的极限不存在。 【分析】观察分子、分母中变量,x y 的各次幂的特点,可考虑选择路径 2x ky =。 证明: 22 24242442000lim (,)lim lim 1y y y x ky x ky xy ky k f x y x y k y y k →→→=====+++, k ∴不同,极限值就不同,故 (,)(0,0) lim (,)x y f x y →不存在。 第十七章多元函数微分学 教学目的: 1.理解多元函数微分学的概念,特别应掌握偏导数、全微分、连续及偏导存在、偏导连续等之间的关系; 2.掌握多元函数特别是二元函数可微性及其应用。 教学重点难点:本章的重点是全微分的概念、偏导数的计算以及应用;难点是复合函数偏导数的计算及二元函数的泰勒公式。 教学时数:18 学时 § 1 可微性 一.可微性与全微分: 1.可微性:由一元函数引入. 亦可写为, 时. 2 .全微分: 例 1 考查函数在点处的可微性. P107 例 1 二. 偏导数: 1.偏导数的定义、记法: 2.偏导数的几何意义: P109 图案17 —1. 3.求偏导数: 例 2 , 3 , 4 . P109 —110 例 2 , 3 , 4 . 例 5 . 求偏导数. 例 6 . 求偏导数. 例7 . 求偏导数, 并求. 例8 . 求和. =. 例9 证明函数在点连续, 并求和. . 在点连续. 三. 可微条件 : 1. 必要条件 : Th 1 设 为函数 定义域的内点 . 在点 可微 和 存在 , 且 . ( 证 ) 由于 , 微分记为 定理 1 给出了计算可微函数全微分的方法 例 10 考查函数 2. 充分条件 : 不存在 两个偏导数存在是可微的必要条件 , 但不充分 . 在原点的可微性 [1]P110 例 5 . Th 2 若函数的偏导数在的某邻域内存在, 且和在 点处连续. 则函数在点可微. (证) P111 Th 3 若在点处连续, 点存在 则函数在点可微. . 即在点可微. 要求至少有一个偏导数连续并不是可微的必要条件. 验证函数在点可微, 但和在点处不连续. (简证, 留为作业) 证 第七章 多元函数微分学 一、内容分析与教学建议 (一) 本章主要是把一元函数微分学中一些主要概念、理论和方法推广到多元函数,一方 面充实微分学,另一方面也给工程技术及自然科学提供一些处理问题的方法和工具。 在教学方法上,在一元函数微分学基础上,通过类比方法引入新的问题、概念、理论和方法,并注意比较它们的异同。 (二) 多元函数、极限、连续 先通过介绍平面点集的几个基础概念,引入二元函数由点函数再过渡到多元函数,并引入多元函数极限,讲清它的概念,并指出二元函数与一元函数极限点0P P →方式的异同,可补充一些简单例题给出二元函数求极限的一些常用方法,如换元化为一元函数两边夹准则,运用连续性等。在理解极限概念之基础上,不难得到求一个二元函数极限不存在之方法,最后可介绍累次极限与重极限之关系。 (三) 偏导数与全微分 1、可先介绍偏增量概念,类比一元函数,引入偏导数,通过例题说明,偏导与连续之关系,在偏导数的计算中,注意讲清分段函数分界点处的偏导数。 2、可由测量矩形相邻边长计算面积实例,类比一元函数的微分,引入全微分的定义,并指出用定义判断),(y x f z =可微,即求极限[ ]ρ y y x z x y x z z y x y x ?+?-?→?→?),(),(lim 0 是 否为0。 3、讲清教材中全微分存在的必要条件和充分条件,重点指出可微与偏导之关系,让学生理解关系式dy y z dx x z dz ??+??= 之意义,最后可通过列表给出多元函数连续、偏导存在、可微之相互关系。 (四) 复合函数求偏导 1、可先证明简单情形的全导数公式,画出函数关系图,通过关系图中“分线相加,连线相乘”法则推广至偏导数或全微分的各种情形),(v u f z =,)(x u ?=,)(x v ?=从中让学生理解口诀的含义。 多元函数微分学复习题及答案 ————————————————————————————————作者:————————————————————————————————日期: 第八章 多元函数微分法及其应用 复习题及解答 一、选择题 1. 极限lim x y x y x y →→+00 242= (提示:令22 y k x =) ( B ) (A) 等于0 (B) 不存在 (C) 等于 12 (D) 存在且不等于0或1 2 2、设函数f x y x y y x xy xy (,)sin sin =+≠=? ????1100 ,则极限lim (,)x y f x y →→0 = ( C ) (提示:有界函数与无穷小的乘积仍为无穷小) (A) 不存在 (B) 等于1 (C) 等于0 (D) 等于2 3、设函数f x y xy x y x y x y (,)=++≠+=??? ? ?22 2222000 ,则(,)f x y ( A ) (提示:①在220x y +≠,(,)f x y 处处连续;②在0,0x y →→ ,令y kx =, 2222 2 lim lim 0(0,0)1x x y kx kx f x k x k →→→===++ ,故在220x y +=,函数亦连续.所以, (,)f x y 在整个定义域内处处连续.) (A) 处处连续 (B) 处处有极限,但不连续 (C) 仅在(0,0)点连续 (D) 除(0,0)点外处处连续 4、函数z f x y =(,)在点(,)x y 00处具有偏导数是它在该点存在全微分的 ( A ) (A)必要而非充分条件 (B)充分而非必要条件 (C)充分必要条件 (D)既非充分又非必要条件 5、设u y x =arctan ,则??u x = ( B ) (A) x x y 22 + (B) - +y x y 22 (C) y x y 22 + (D) -+x x y 22 6、设f x y y x (,)arcsin =,则f x '(,)21= ( A ) (A )- 14 (B )14 (C )-12 (D )1 2 第七章 多元函数微分学 【内容提要】 1.空间解析几何基础知识 三条相互垂直的坐标轴Ox 、Oy 、Oz 组成了一个空间直角坐标系。 空间直角坐标系下两点间的距离公式为: 平面方程:0Ax By Cz D +++= 二次曲面方程: 2220Ax By Cz Dxy Eyz Fzx Gx Hy Iz K +++++++++= 球面方程:()()()2 2 02 02 0R z z y y x x =-+-+- 圆柱面方程:2 22R y x =+ 椭球面方程:()222 2221,,0x y z a b c a b c ++=>, 椭圆抛物面方程:22 22,(,0)x y z a b a b +=> 双曲抛物面方程:22 22,(,0)x y z a b a b -=> 单叶双曲面图方程:122 2222=-+c z b y a x (a ,b ,c >0) 双叶双曲面方程:222 2221,(,,0)x y z a b c a b c +-=-> 椭圆锥面方程:222 2220,(,,0)x y z a b c a b c +-=> 2.多元函数与极限 多元函数的定义:在某一过程中,若对变化范围D 的每一对值(,)x y ,在变域M 中存在z 值,按一定对应法则f 进行对应,有唯一确定的值,则称f 为集合D 上的二元函数, 记为 ,x y 称为自变量,D 称为定义域,z 称为因变量。(,)x y 的对应值记为(,)f x y ,称为函数 值,函数值的集合称为值域。 多元函数的极限:设函数(,)f x y 在开区间(或闭区间)D 内有定义,000(,)P x y 是D 的内点或边界点。如果对于任意给定的正数e ,总存在正数d ,使得对于适合不等式 的一切点(,)P x y D ?,都有 第九章 多元函数微分法及其应用高等数学教案ch 8 多元函数微分法及其应用
多元函数微分学总结
(完整word版)(整理)数学分析教案(华东师大版)第十七章多元函数微分学
第七章多元函数微分高等数学
多元函数微分学复习题及标准答案
多元函数微分学习题
第九章多元函数微分法及其应用教案
【教学目标与要求】
1、 理解多元函数的概念和二元函数的几何意义。
2、 了解二元函数的极限与连续性的概念,以及有界闭区域上的连续函数的性质。
3、 理解多元函数偏导数和全微分的概念,会求全微分,了解全微分存在的必要条件和充分条件,
了解全微分形式的不变性。
4、 理解方向导数与梯度的概念并掌握其计算方法。
5、掌握多元复合函数偏导数的求法。
6、会求隐函数(包括由方程组确定的隐函数)的偏导数。
7、了解曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程。
8、了解二元函数的二阶泰勒公式。
9、理解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极
值存在的充分条件,会求二元函数的极值,会用拉格郎日乘数法求条件极值,会求简多元函数的最大
值和最小值,并会解决一些简单的应用问题。
【教学重点】
1、 二元函数的极限与连续性;
2、 函数的偏导数和全微分;
3、 方向导数与梯度的概念及其计算;
4、 多元复合函数偏导数;
5、 隐函数的偏导数;多元函数极值和条件极值的求法;
6、 曲线的切线和法平面及曲面的切平面和法线;
【教学难点】
1、 二元函数的极限与连续性的概念;
2、全微分形式的不变性;
3、复合函数偏导数的求法;
4、二元函数的二阶泰勒公式;
5、隐函数(包括由方程组确定的隐函数)的偏导数;
6、 拉格郎日乘数法,多元函数的最大值和最小值。
【教学课时分配】 (18 学时)
第 1 次课 §1 第 2 次课 §2
第 3 次课 §3
第 4 次课 §4
第 5 次课 §5
第 6 次课
§6
第 7 次课 §7
第 8 次课 §8
第 9 次课
习题课
【参考书】
[1]同济大学数学系.《高等数学(下)》,第五版.高等教育出版社.
[2] 同济大学数学系.《高等数学学习辅导与习题选解》,第六版.高等教育出版社.
[3] 同济大学数学系.《高等数学习题全解指南(下)》,第六版.高等教育出版社
